(年贵州黔西南16分)如图所示,在平面直角坐标系中,抛物线y=ax2+bx+c经过A(﹣3,0)、B(1,0)、C(0,3)三点,其顶点为D,连接AD,点P是线段AD上一个动点(不与A、D重合),过点P作y轴的垂线,垂足点为E,连接AE.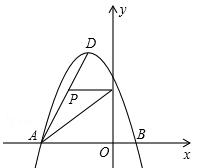
(1)求抛物线的函数解析式,并写出顶点D的坐标;
(2)如果P点的坐标为(x,y),△PAE的面积为S,求S与x之间的函数关系式,直接写出自变量x的取值范围,并求出S的最大值;
(3)在(2)的条件下,当S取到最大值时,过点P作x轴的垂线,垂足为F,连接EF,把△PEF沿直线EF折叠,点P的对应点为点P′,求出P′的坐标,并判断P′是否在该抛物线上.
用长为20cm的铁丝,折成一个矩形,设它的一边长为xcm,面积为ycm2。
(1)求出y与x的函数关系式
(2)当边长x为多少时,矩形的面积最大,最大面积是多少?
如图,正方形网格中,△ABC 为格点三角形(顶点都是格点),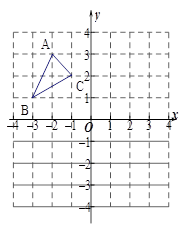
(1)将△ABC绕点O按逆时针方向旋转90°得到△
(2)将△ABC绕原点O旋转180°,画出旋转后的△
已知:关于x的方程x2-2(m+1)x+m2=0.
(1)当m取何值时,方程有两个实数根?
(2)为m选取一个合适的整数,使方程有两个不相等的实数根,并求这两个根.
用适当的方法解下列方程:
(1)
(2)x2-4x+1=0
在直角坐标平面中,已知点A(10,0)和点D(8,0).点C、B在以OA为直径的⊙M上,且四边形OCBD为平行四边形.
(1)求C点坐标;
(2)求过O、C、B三点的抛物线解析式
(3)判断:(2)中抛物线的顶点与⊙M的位置关系,说明理由.