(年新疆区、兵团12分)如图,直线 与x轴交于A点,与y轴交于B点,动点P从A点出发,以每秒2个单位的速度沿AO方向向点O匀速运动,同时动点Q从B点出发,以每秒1个单位的速度沿BA方向向点A匀速运动,当一个点停止运动,另一个点也随之停止运动,连接PQ,设运动时间为t(s)(0<t≤3).
与x轴交于A点,与y轴交于B点,动点P从A点出发,以每秒2个单位的速度沿AO方向向点O匀速运动,同时动点Q从B点出发,以每秒1个单位的速度沿BA方向向点A匀速运动,当一个点停止运动,另一个点也随之停止运动,连接PQ,设运动时间为t(s)(0<t≤3).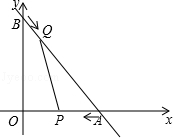
(1)写出A,B两点的坐标;
(2)设△AQP的面积为S,试求出S与t之间的函数关系式;并求出当t为何值时,△AQP的面积最大?
(3)当t为何值时,以点A,P,Q为顶点的三角形与△ABO相似,并直接写出此时点Q的坐标.
如图,方形ABCD的AB边为直径,在正方形内部作半圆,圆心为O,DF切半圆于点E,交AB的延长线于点F,BF=4.求:
(1). cos∠F的值;
(2). BE的长.
某省为解决农村饮用水问题,省财政部门共投资20亿元对各市的农村饮用水的“改水工程”予以一定比例的补助.2008年,A市在省财政补助的基础上投入600万元用于“改水工程”,计划以后每年以相同的增长率投资,2010年该市计划投资“改水工程”1176万元.
(1). 求A市投资“改水工程”的年平均增长率;
(2). 从2008年到2010年,A市三年共投资“改水工程”多少万元?600+600×1.4+1176=2616(万元).A市三年共投资
已知:直线a∥b,点A、B在直线a上,点C、D在直线b上,如图
(1). 若 ,则
,则

(2). 若 ,那么
,那么 吗?说明你的理由。
吗?说明你的理由。
某单位欲招聘一名员工,现有 三人竞聘该职位,他们的笔试成绩和口试成绩(单位:分)分别用两种方式进行了统计,如表一和图一.
三人竞聘该职位,他们的笔试成绩和口试成绩(单位:分)分别用两种方式进行了统计,如表一和图一.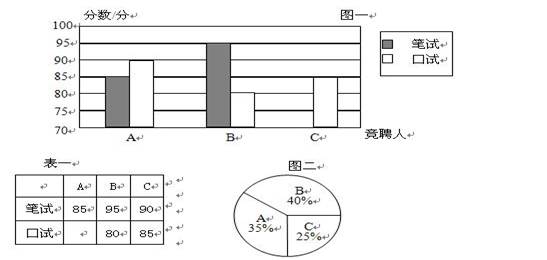
(1). 请将表一和图一中的空缺部分补充完整;
(2). 竞聘的最后一个程序是由该单位的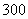 名职工进行投票,三位竞聘者的得票情
名职工进行投票,三位竞聘者的得票情
(3). 若每票计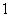 分,该单位将笔试、口试、得票三项测试得分按
分,该单位将笔试、口试、得票三项测试得分按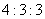 的比例确定 个人成绩,请计算三位竞聘者的最后成绩,并根据成绩判断谁能竞聘成功.
的比例确定 个人成绩,请计算三位竞聘者的最后成绩,并根据成绩判断谁能竞聘成功.
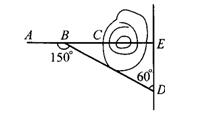
建设中的昆石高速公路,在某施工段上沿AC方向开山修路,为加快施工速度,要在山坡的另一边同时施工,如图所示,从AC上的一点B取∠ABD=150°,BD=380米,∠D=60°,那么开挖点E离D多远,正好使A、C、E成一直线.