（年湖北黄冈13分）如图，在四边形OABC中，AB∥OC，BC⊥x轴于C，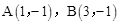
，动点P从O点出发，沿x轴正方向以2个单位/秒的速度运动．过P作PQ⊥OA于Q．设P点运动的时间为t秒（0 < t < 2），ΔOPQ与四边形OABC重叠的面积为S．
（1）求经过O、A、B三点的抛物线的解析式并确定顶点M的坐标；
（2）用含t的代数式表示P、Q两点的坐标；
（3）将ΔOPQ绕P点逆时针旋转90°，是否存在t，使得ΔOPQ的顶点O或Q落在抛物线上？若存在，直接写出t的值；若不存在，请说明理由；
（4）求S与t的函数解析式.
如图，在
和
中，
、
交于点M.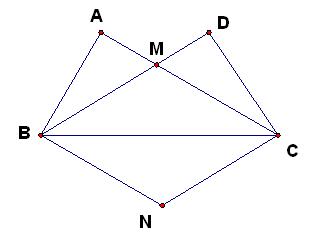
（1）求证：≌；
（2）作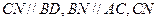
交
于点N，四边形BNCM是什么四边形？请证明你的结论.
请你先化简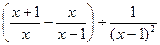
，再从0，
， 2，1中选择一
个合适的数代入，求出这个代数式的值.
已知，边长为5的正方形ABCO在如图所示的直角坐标系中，点
M（t，0）为x轴上一动点，过A作直线MC的垂线交y轴于点N．
（1）当t=2时，求直线MC的解析式；
（2）设△AMN的面积为S，当S＝3时，求t的值；
（3）取点P（1，y），如果存在以M、N、C、P为顶点的四边形是等腰梯形，当t＜0时，甲同学说：y与t应同时满足方程t2－yt－5＝0和y2－2t2－10y＋26＝0；乙同学说：y与t应同时满足方程t2－yt－5＝0和y2＋8t－24＝0，你认为谁的说法
正确，并说明理由．再直接写出t＞0时满足题意的一个点P的坐标．
如图，抛物线F：y＝ax2＋bx＋c的顶点为P，抛物线F与
轴交于点A，
过点P作PD⊥x轴于点D，平移抛物线F使其经过点A、D得
到抛物线F ′：
y＝a′x2＋b′x＋c′，抛物线F ′与x轴的另一个交点为C．
（1）当a＝1，b＝－2，c＝3时，
①写出点D的坐标▲；②求b: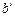
的值；
（2）若a、b、c满足b2＝ac，探究b: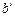的值是否为定值？若是定值请求出这个定值；若不是请说明理由．
某年级组织学生参加数理化奥林匹克竞赛的培训，下面两幅统计图反
映了学生自愿报名（每人限报一科）的情况，请你根据图中信息回答下列问题：
（1）该年级报名参加数学培训的人数有▲．
（2）该年级报名参加这三科奥训的总人数是▲．请补全条形统计图．
（3）根据实际情况，需从数学组抽调部分同学到化学组，使化学组人数是数学组人数的3倍，则应从数学组抽调多少名学生？