（年山东菏泽10分）在平面直角坐标系xOy，已知抛物线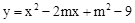
．
（1）求证：无论m为何值，该抛物线与x轴总有两个交点；
（2）该抛物线与x轴交于A，B两点，点A在点B的左侧，且OA＜OB，与y轴的交点坐标为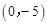
，求此抛物线的解析式；
（3）在（2）的条件下，抛物线的对称轴与x轴的交点为N，若点M是线段AN上的任意一点，过点M作直线MC⊥x轴，交抛物线于点C，记点C关于抛物线对称轴的对称点为D，点P是线段MC上一点，且满足MP=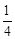
MC，连结CD，PD，作PE⊥PD交x轴与点E，问是否存在这样的点E，使得PE=PD，若存在，求出点E的坐标；若不存在，请说明理由．
如图所示：直线AB∥CD，DE∥BC，∠B=（2x+10）°，∠D=（60-3x）°，
求x的值及∠BCD的度数。
有首诗说的是《西游记》中孙悟空的故事：
悟空顺风探妖踪，千里只用四分钟；归时四分行六百，风速多少才算准。
根据以上内容求出风速是每分多少里？
当m取什么整数时，关于x的方程
的解是正整数。
解方程：（每题4分，共16分）
（1）
-
-
=1
已知抛物线的顶点为P（－4，－
），与x轴交于A、B两点，与y轴交于点C，其中B点坐标为（1，0）
（1）求这条抛物线的函数关系式；
（2）若抛物线的对称轴交x轴于点D，则在线段AC上是否存在这样的点Q，使得△ADQ为等腰三角形？若存在，请求出符合条件的点Q的坐标；若不存在，请说明理由．