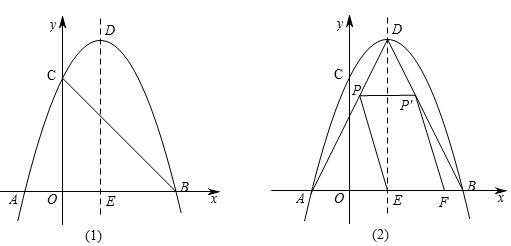
（2014年广西河池12分）如图（1），在平面直角坐标系xOy中，抛物线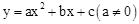
与x轴交于
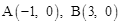，与y轴交于C(0，3)，顶点为D(1,4)，对称轴为DE.
（1）抛物线的解析式是 ；
（2）如图（2），点P是AD上的一个动点，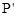
是P关于DE的对称点，连结PE，过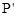作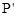F∥PE交x轴于F. 设
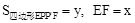，求y关于x的函数关系式，并求y的最大值；
（3）在（1）中的抛物线上是否存在点Q，使△BCQ成为以BC为直角边的直角三角形？若存在，求出Q的坐标；若不存在，请说明理由.
如图，是儿童乐园平面图．请建立适当的平面直角坐标系，写出儿童乐园中各娱乐设施的坐标．
按照下列条件确定点
位置：
⑴ 若x=0,y≥0，则点P在 .
⑵ 若xy=0，则点P在 .
⑶ 若
，则点P在.
⑷ 若
，则点P 在 .
⑸ 若
，则P在 .
在如图所示的平面直角坐标系中描出A（2 3），B（-3，-2），C（4，1）三点，并用线段将A、B、C三点依次连接起来，你能求出它的面积吗？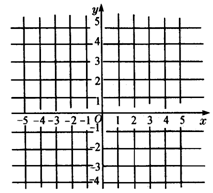
已知点A（a-1，2），B（-3，b+1）,根据下列要求确定a、b的值：
（1）直线AB∥x轴.
（2）直线AB∥y轴.
（3）AB两点在第一、三象限的角平分线上.
在直角坐标系中设法找到若干个点,使得连结各点所得的封闭图形是如图所示的“+”字.