（2014年黑龙江大庆3分）对坐标平面内不同两点A（x1，y1）、B（x2，y2），用|AB|表示A、B两点间的距离（即线段AB的长度），用║AB║表示A、B两点间的格距，定义A、B两点间的格距为║AB║=|x1﹣x2|+|y1﹣y2|，则|AB|与║AB║的大小关系为（ ）
A．|AB|≥║AB║ B．|AB|＞║AB║ C．|AB|≤║AB║ D．|AB|＜║AB║
下列运算正确的是（）
A． |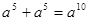
B． |
C． |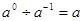
D． |
连结多边形不相邻的两个顶点的线段，叫做多边形的对角线．观察上述图形并阅读相关文字，思考回答问题：显然四边形对角线有2条；五边形的对角线有5条；对于六边形的对角线条数，光靠“数”数，也能数出来，但已感到较麻烦！需寻找规律！从一个顶点A出发，显然有3条，同理从B出发也3条，每个顶点出发都是3条，但从C顶点出发，就有重复线段！用此方法算出六边形的对角线条数为a；且能归纳出n边形的对角线条数的计算方法；若一个n边形有35条对角线，则a和n的值分别为（）
| A．12，20 | B．12，15 | C．9，10 | D．9，12 |
已知
，则下列结论正确的是（）
| A．2m－n＝1 | B．2m－n＝3 | C．2m＋n＝3 | D．2m＝3n |
已知a，b，c是三角形的三边，那么代数式
的值（）
| A．大于零 | B．小于零 | C．等于零 | D．不能确定 |
下列各式中，不能用平方差公式计算的是（ ）
A． |
B． |
C． |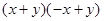
D． |