已知:y关于x的函数 的图象与x轴有交点。
的图象与x轴有交点。
(1)求k的取值范围;
(2)若x1,x2是函数图象与x轴两个交点的横坐标,且满足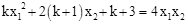 .
.
①求k的值;②当 时,请结合函数图象确定y的最大值和最小值。
时,请结合函数图象确定y的最大值和最小值。
如 图所示,是正方体展开图的各面编号,指出相对两面的号码组合(相对面没有公共棱),再指出与面6相邻的面.
图所示,是正方体展开图的各面编号,指出相对两面的号码组合(相对面没有公共棱),再指出与面6相邻的面.
连线题
把图中第一行的展开图与第二行中相对应的几何体用线连接起来.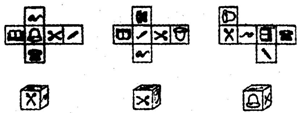
如图,∠AOB为直角,∠BOC为锐角,且OM平分∠AOC,ON平分∠BOC.
⑴.若∠BOC=46°,试求∠MON的度数;
⑵.如果⑴中的∠BOC=α(α为锐角),其他条件不变,
试求∠MON的度数(结果用含α的式子表示).
⑶.如果∠AOB=β,∠BOC=46°其他条件不变,
试求∠M ON的度数(结果用含β的式子表示).
ON的度数(结果用含β的式子表示).
我校要刻录一批电脑光盘,若到电脑公司刻录,每张需要8元;若学校自己刻,除租用刻录机需要120元外,每张还需要成本4元。
⑴.刻录多少张光盘时,到电脑公司刻录与学校自己刻录所需费用一样?
⑵.刻录多少张光盘时,到电脑公司刻录较合算?⑶.刻录多少张光盘时,学校自己刻录较合算?
如图,已知点C为AB上的一点,AC=12㎝,CB=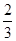 AC,D、E分别为AC、AB的中点,求DE的长.
AC,D、E分别为AC、AB的中点,求DE的长.
 |