如图，在平面直角坐标系中，O为坐标原点，点A、B的坐标分别为（8，0）、（0，6）．动点Q从点O、动点P从点A同时出发，分别沿着OA方向、AB方向均以1个单位长度/秒的速度匀速运动，运动时间为t（秒）（0＜t≤5）．以P为圆心，PA长为半径的⊙P与AB、OA的另一个交点分别为点C、D，连结CD、QC．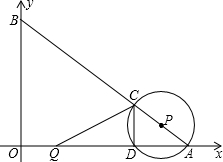
（1）当t为何值时，点Q与点D重合？
（2）当t为何值时，DQ=2AD？
（3）求线段QC所在直线与⊙P相切时t的值。
已知一次函数的图象经过点（3，5）与（－4，－9）．
（1）求这个函数的解析式；
（2）判断点A（1，－1）和点B（2.5，4）是否在这个函数的图象上．
△ABC在平面直角坐标系中的位置如右图所示．
（1）直接写出点A的坐标；
（2）作出△ABC关于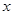
轴对称的△
，并分别写出点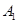
，B1，C1的坐标
（1）解方程：
；（2）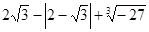
老王带上若干千克自产的土豆进城出售，为了方便，他带了一些零钱备用，按市场价售出一 些后，又降价出售，售出的土豆千克数与他手中持有的钱数(含备用零钱)的关系，如图所示，结合图象回答下列问题．
(1)老王自带的零钱是多少？
(2)试求降价前y与x之间的关系式．
(3)由表达式你能求出降价前每千克的土豆价格是多少？
(4)降价后他按每千克0.4元将剩余土豆售完，这时他手中的钱(含备用零钱)是26元，试问他一共带了多少千克土豆？
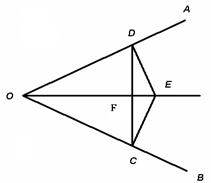
如图，已知：E是∠AOB的平分线上一点，EC⊥OB，ED⊥OA，C、D是垂足，连接CD，且交OE于点F．
（1）求证：OE是CD的垂直平分线．
（2）若∠AOB＝60º，请你探究OE，EF之间有什么数量关系？并证明你的结论．