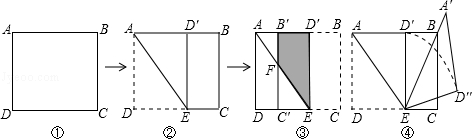
如图①，在矩形纸片ABCD中，AB=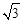
+1，AD=．
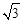（1）如图②，将矩形纸片向上方翻折，使点D恰好落在AB边上的D′处，压平折痕交CD于点E，则折痕AE的长为 ；
（2）如图③，再将四边形BCED′沿D′E向左翻折，压平后得四边形B′C′ED′，B′C′交AE于点F，则四边形B′FED′的面积为 ；
（3）如图④，将图②中的△AED′绕点E顺时针旋转α角，得△A′ED″，使得EA′恰好经过顶点B，求弧D′D″的长．（结果保留π）
如图，在等腰Rt△ABC中，∠ACB=90°，AC=CB，F是AB边上的中点，点D、E分别在边AC、BC边上，且AD=CE．连接DE、DF、EF．
（1）求证：△ADF≌△CEF
（2）试判断△DFE的形状，并说明理由．
已知：如图，AB=AD，∠D=∠B，∠1=∠2，求证：（1）△ADE≌△ABC；（2）∠DEB=∠2．
如图，AB=EF，BC⊥AE于C，FD⊥AE于D，CE=DA．
求证：（1）△ABC≌△EFD；
（2）AB//EF．
如图，CD平分△ABC的外角∠BCE，且CD//AB，求证：AC=BC
已知：如图，已知△ABC，分别画出与△ABC关于
轴、
轴对称的图形△A1B1C1和△A2B2C2．