如图，A、B两点的坐标分别是（8，0）、（0，6），点P由点B出发沿BA方向向点A作匀速直线运动，速度为每秒3个单位长度，点Q由A出发沿AO（O为坐标原点）方向向点O作匀速直线运动，速度为每秒2个单位长度，连接PQ，若设运动时间为t（0＜t＜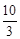
）秒．解答如下问题：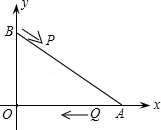
（1）当t为何值时，PQ∥BO？
（2）设△AQP的面积为S，
①求S与t之间的函数关系式，并求出S的最大值；
②若我们规定：点P、Q的坐标分别为（x1，y1），（x2，y2），则新坐标（x2﹣x1，y2﹣y1）称为“向量PQ”的坐标．当S取最大值时，求“向量PQ”的坐标．
中，
，
的面积．
轴的对称图形
．
的坐标．
，其中