(本小题满分12分)如图,在四棱锥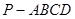 中,平面PAD⊥平面ABCD,AB=AD,∠BAD=60°,E、F分别是AP、AD的中点
中,平面PAD⊥平面ABCD,AB=AD,∠BAD=60°,E、F分别是AP、AD的中点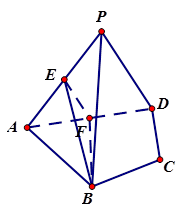
求证:(1)直线EF∥平面PCD;
(2)平面BEF⊥平面PAD
(本小题满分12分)
某公司今年年初用25万元引进一种新的设备,投入设备后每年收益为21万元。该公司第n年需要付出设备的维修和工人工资等费用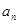 的信息如图,其中点
的信息如图,其中点 落在一条直线上.
落在一条直线上.
(1)求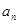 ;
;
(2)引进这种设备后,第几年后该公司开始获利;
(3)这种设备使用多少年,该公司的年平均获利最大?
(本小题满分12分)
已知△ABC的内角A、B、C的对边分别为a,b,c,已知a=bcosC+csinB.
(1)求B;
(2)若b=2,求△ABC面积的最大值.
(本小题满分12分)
已知函数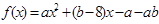 ,且不等式
,且不等式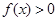 的解集为
的解集为 ;
;
(1)求函数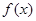 的解析式;
的解析式;
(2)c为何值时,关于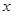 的不等式
的不等式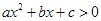 无解.
无解.
(本小题满分10分)
在△ABC中,  是方程
是方程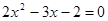 的一个根,
的一个根,
(1)求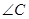 ;
;
(2)当 时,求△ABC周长的最小值.
时,求△ABC周长的最小值.
(本小题满分14分)
已知 是椭圆
是椭圆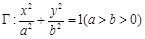 的左右焦点,椭圆
的左右焦点,椭圆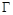 的离心率
的离心率 ,
, 是
是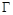 上异于左右顶点的任意一点,且
上异于左右顶点的任意一点,且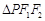 的面积的最大值为1.
的面积的最大值为1.
(Ⅰ)求椭圆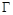 的方程;
的方程;
(Ⅱ)直线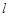 是椭圆在点P处的切线,过
是椭圆在点P处的切线,过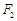 作
作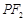 的垂线,交直线
的垂线,交直线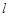 相交于Q,求证:点Q落在一条定直线
相交于Q,求证:点Q落在一条定直线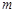 上,并求直线
上,并求直线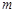 的方程.
的方程.