如图,4×4的方格中每个小正方形的边长都是1,则S四边形ABCD与S四边形ECDF的大小关系是( )
| A.S四边形ABDC=S四边形ECDF | B.S四边形ABDC<S四边形ECDF |
| C.S四边形ABDC=S四边形ECDF+1 | D.S四边形ABDC=S四边形ECDF+2 |
如图,每个小正方形边长均为1,则下列阴影部分的三角形与左图中△ABC相似的是( )
如图,A、B两点被池塘隔开,在AB外任选一点C,连结AC、BC分别取其三等分点M、N量得 MN=38m.则AB的长是( ) 
A.152mB.114m
C.76mD.104m
下列命题中,假命题的是:( )
| A.对顶角的平分线成一条直线 | B.对顶角相等 |
| C.不是对顶角的两个角不相等 | D.不相等的两个角不是对顶角 |
若△ABC∽△DEF,且面积比为1 :9,则△ABC与△DEF的周长比为( )
| A.1 :3 | B.1 :9 | C.3 :1 | D.1 :81 |
已知点C是线段AB的黄金分割点,且AC>BC,则下列等式中正确的是( )
A.AB2=AC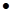 BC BC |
B.BC2=AC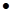 AB AB |
C.AC2=BC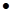 AB AB |
D.AC2=2AB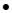 BC BC |