(本题10分)如图1,矩形ABCD中,点P从A出发,以3cm/s的速度沿边A→B→C→D→A匀速运动;同时点Q从B出发,沿边B→C→D匀速运动,当其中一个点到达终点时两点同时停止运动,设点P运动的时间为t s.△APQ的面积s(cm2)与t(s)之间函数关系的部分图像由图2中的曲线段OE与线段EF给出.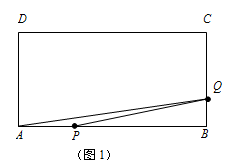
(1)点Q运动的速度为 cm/s,a﹦ cm2;
(2)若BC﹦3cm,① 求t>3时S的函数关系式;② 在图(2)中画出①中相应的函数图像.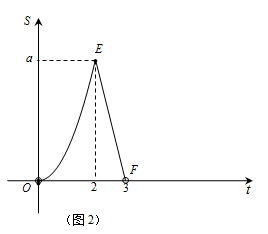
受国际原油价格持续上涨影响,某市对出租车的收费标准进行调整.
(1)调整前出租车的起步价为 ▲ 元,超过3km收费 ▲元/km;
(2)求调整后的车费y(元)与行驶路程x(km)(x>3)之间的函数关系式,并在图中画出其函数图象.
某初级中学准备随机选出七、八、九三个年级各1名学生担任领操员.现已知这三个年级分别选送一男、一女共6名学生为备选人.(1)请你利用树状图或表格列出所有可能的选法;
(2)求选出“两男一女”三名领操员的概率.
某区为了解全区2800名九年级学生英语口语考试成绩的情况,从中随机抽取了部分学生的成绩(满分24分,得分均为整数),制成下表:
| 分数段(x分) |
x≤16 |
17≤x≤18 |
19≤x≤20 |
21≤x≤22 |
23≤x≤24 |
| 人数 |
10 |
15 |
35 |
112 |
128 |
(1)填空:
①本次抽样调查共抽取了 ▲名学生;
②学生成绩的中位数落在▲分数段;
③若用扇形统计图表示统计结果,则分数段为x≤16的人数所对应扇形的圆心角为 ▲°;(2)如果将21分以上(含21分)定为优秀,请估计该区九年级考生成绩为优秀的人数.
如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,AE∥BC, DE∥AB.
证明:(1)AE=DC;(2)四边形ADCE为矩形.
先化简,再求值: ,其中a=-2,b=
,其中a=-2,b= .
.