如图，正方形ABCD中，以BC为直径作半圆，BC=2㎝．现有两动点E、F，分别从点B、点A同时出发，点E沿线段BA以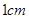
/秒的速度向点A运动，点F沿折线A→D→C以
/秒的速度向点C运动．当点E到达A点时，E、F同时停止运动，设点E运动时间为
．
（1）当为何值时，线段EF与BC平行？
（2）设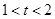
，当为何值时，EF与半圆相切？
（3）如图2，将图形放在直角坐标系中，当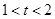时，设EF与AC相交于点P，双曲线
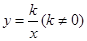经过点P，并且与边AB交于点H，求出双曲线的函数关系式，并直接写出
的值．
有两个不同形状的计算器（分别记为A，B）和与之匹配的保护盖（分别记为a，b）（如图所示）散乱地放在桌子上．
（1）若从计算器中随机取一个，再从保护盖中随机取一个，求恰好匹配的概率．
（2）若从计算器和保护盖中随机取两个，用树形图法或列表法，求恰好匹配的概率．
“初中生骑电动车上学”的现象越来越受到社会的关注，某校利用“五一”假期，随机抽查了本校若干名学生和部分家长对“初中生骑电动车上学”现象的看法，统计整理制作了如下的统计图，请回答下列问题：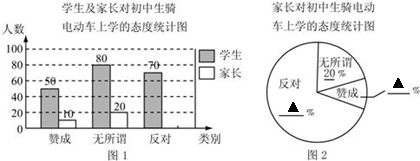
⑴这次共抽查了个家长；
⑵请补全条形统计图和扇形统计图（友情提醒：条形图补画家长持“反对”态度的人数条，扇形图填上“反对”及“赞成”的百分数）；
⑶已知该校共有1200名学生，持“赞成”态度的学生估计约有人．
如图，在
ABCD中，E、F为对角线BD上的两点，且∠BAE=∠DCF．求证：BE=DF．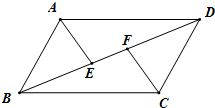
（1）解方程：
（2）解不等式组：
（1）计算：
（2）化简
．