(本小题满分14分)
在平面直角坐标系xoy中,椭圆C :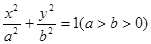 的离心率为
的离心率为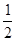 ,右焦点F(1,0),点P在椭圆C上,且在第一象限内,直线PQ与圆O:
,右焦点F(1,0),点P在椭圆C上,且在第一象限内,直线PQ与圆O: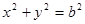 相切于点M.
相切于点M.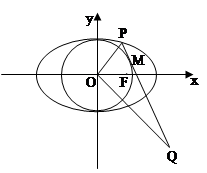
(1)求椭圆C的方程;
(2)求|PM|·|PF|的取值范围;
(3)若OP⊥OQ,求点Q的纵坐标t的值.
如图,四边形ABCD中,AB⊥AD,AD∥BC,AD=6,BC=4,AB=2,E、F分别在BC、AD上,EF∥AB.现将四边形ABEF沿EF折起,使得平面ABEF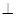 平面EFDC.
平面EFDC.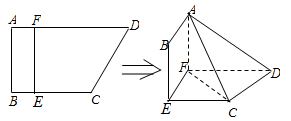
(1)当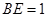 ,是否在折叠后的AD上存在一点
,是否在折叠后的AD上存在一点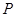 ,使得CP∥平面ABEF?若存在,求出P点位置,若不存在,说明理由;
,使得CP∥平面ABEF?若存在,求出P点位置,若不存在,说明理由;
(2)设BE=x,问当x为何值时,三棱锥A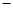 CDF的体积有最大值?并求出这个最大值.
CDF的体积有最大值?并求出这个最大值.
(本小题满分12分)在 中,已知角A、B、C所对的边分别为
中,已知角A、B、C所对的边分别为 ,直线
,直线 与直线
与直线 互相平行(其中
互相平行(其中 ).
).
(1)求角A的值;
(2)若 的取值范围.
的取值范围.
(本小题满分12分)“等比数列  中,
中, ,且
,且  是
是  和
和  的等差中项,若
的等差中项,若 
(1)求数列  的通项公式;
的通项公式;
(2)求数列 的前
的前 项和.
项和.
(不等式选讲)(本小题满分10分)设函数
(1)求不等式 的解集;
的解集;
(2)若不等式

 的解集非空,求实数
的解集非空,求实数 的取值范围.
的取值范围.
(极坐标与参数方程选讲)(本小题满分10分)在平面直角坐标系中,以坐标原点为极点,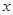 轴的非负半轴为极轴建立坐标系.已知点
轴的非负半轴为极轴建立坐标系.已知点 的极坐标为
的极坐标为 ,直线的极坐标方程为
,直线的极坐标方程为 ,且点
,且点 在直线上.
在直线上.
(1)求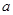 的值及直线的直角坐标方程;
的值及直线的直角坐标方程;
(2)圆 的参数方程为
的参数方程为 ,(
,( 为参数),试判断直线与圆的位置关系.
为参数),试判断直线与圆的位置关系.