【阅读理解】对于任意正实数a、b,因为 ≥0,所以
≥0,所以
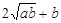 ≥0,所以
≥0,所以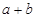 ≥
≥ ,只有当a=b时,等号成立.
,只有当a=b时,等号成立.
【获得结论】在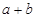 ≥2
≥2 (a、b均为正实数)中,若ab为定值p,则
(a、b均为正实数)中,若ab为定值p,则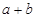 ≥2
≥2 ,只有当a=b时,
,只有当a=b时,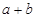 有最小值2
有最小值2 .
.
根据上述内容,回答下列问题:若 >0,只有当
>0,只有当 = 时,
= 时, +
+ 有最小值 .
有最小值 .
【探索应用】如图,已知A(-3,0),B(0,-4),P为 双曲线 上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D。求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.
上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D。求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.
如图,在△ABC中,AD⊥BC,垂足为D,∠B=60°,∠C=45°.
(1)求∠BAC的度数.
(2)若AC=2,求AD的长.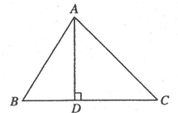
如图,已知:等腰梯形ABCD中,AD∥BC,AB=CD,E、F、G、H分别是AD、BC、BE、CE的中点
(1)求证:△ABE≌△DCE
(2)四边形EGFH是什么特殊四边形?并证明你的结论.
(3)连接EF,当四边形EGFH是正方形时,线段EF与GH有什么数量关系?请说明理由.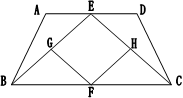
(1)计算: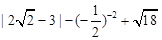 .
.
(2)先化简,在求值: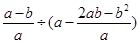 ,其中
,其中 ,
,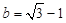 .
.
列方程组或不等式解应用题
在数字化校园建设工程中,某学校计划购进一批笔记本电脑和台式机,经过市场调研得知如下信息:购买1台笔记本和2台台式机需付费1.4万元;购买2台笔记本和1台台式机需付费1.3万元.
(1)求购买一台笔记本和一台台式机各需多少钱(单位:万元)?
(2)根据学校实际情况,计划购进笔记本和台式机共20台.其中,台式机至少10台,笔记本至少8台.请你通过计算求出有几种购买方案,说明哪种费用最低.
阅读学习: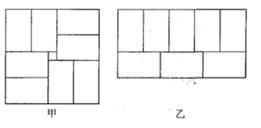
数学中有很多等式可以用图形的面积来表示.如图1,它表示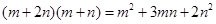 ,
,
(1)观察图2,请你写出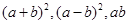 之间的关系________________________.
之间的关系________________________.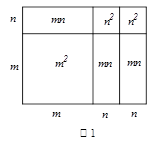
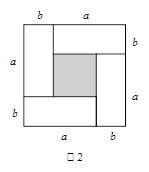
(2)小明用8个一样大的长方形,(长为a,宽为b),拼成了如图甲乙两种图案,图案甲是一个正方形,图案甲中间留下了一个边长为2的正方形;图形乙是一个长方形.则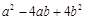 ="___________"
="___________"