如图,若干个全等的正五边形排成环状,图中所示的是前3个正五边形,要完成这一圆环还需正五边形的个数为 ( )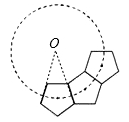
| A.7 | B.8 | C.9 | D.10 |
学校运动会长跑比赛中,张华跑在前面,离终点100米时,在他身后10米的李明想以4米/秒的速度冲刺超过张华,假设这时张华需以x米/秒的速度进行以后的冲刺,这样才能在到达终点时始终保持领先位置,则下列满足题意的不等式为( )
A.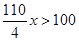 |
B.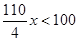 |
C.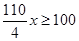 |
D.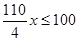 |
据扬子晚报报道,2012年5月7日南京市最高气温是33℃,最低气温是22℃,则当天南京市气温t(℃)的变化范围可用不等式表示为( )
| A.t≥22 | B.t≤22 | C.22<t<33 | D.22≤t≤33 |
亮亮准备用自己节省的零花钱买一台英语复读机,他现在已存有45元,计划从现在起以后每个月节省30元,直到他至少有300元.设x个月后他至少有300元,则可以用于计算所需要的月数x的不等式是( )
| A.30x﹣45≥300 | B.30x+45≥300 | C.30x﹣45≤300 | D.30x+45≤300 |
x的2倍减3的差不大于1,列出不等式是( )
| A.2x﹣3≤1 | B.2x﹣3≥1 | C.2x﹣3<1 | D.2x﹣3>1 |
用甲、乙两种原料配制成某种饮料,已知这两种原料的维生素C含量及购买这两种原料的价格如下表:
| 甲种原料 |
乙种原料 |
|
| 维生素C含量(单位•千克) |
600 |
100 |
| 原料价格(元•千克) |
8 |
4 |
现配制这种饮料10kg,要求至少含有4200单位的维生素C,若所需甲种原料的质量为xkg,则x应满足的不等式为( )
A.600x+100(10﹣x)≥4200
B.8x+4(100﹣x)≤4200
C.600x+100(10﹣x)≤4200
D.8x+4(100﹣x)≥4200