(本小题满分14分)
某地区有小学21所,中学14所,大学7所,现采用分层抽样的方法从这些学校中抽取6所学校对学生进行视力调查.
(1)求应从小学、中学、大学中分别抽取的学校数目;
(2)若从抽取的6所学校中随机抽取2所学校做进一步数据分析.
(ⅰ)列出所有可能的抽取结果;
(ⅱ)求抽取的2所学校均为小学的概率.
如图,在底面是直角梯形的四棱锥P—ABCD中,AD∥BC,∠DAB=90º,PA⊥平面ABCD,PA=AB=BC=1,AD=2,M是PD的中点。
(1)求证:MC∥平面PAB;
(2)在棱PD上求一点Q,使二面角Q—AC—D的正切值为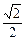 。
。
已知数列 、
、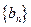 满足:
满足: ,
, ,
,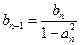 。
。
(1)求数列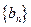 的通项公式;
的通项公式;
(2)若 ,求数列{
,求数列{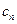 }的前n项和
}的前n项和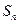 。
。
已知函数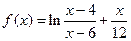
(1)求 的单调区间以及极值;
的单调区间以及极值;
(2)函数 的图像是否为中心对称图形?如果是,请给出严格证明;如果不是,请说明理由。
的图像是否为中心对称图形?如果是,请给出严格证明;如果不是,请说明理由。
设锐角△ABC的三内角A、B、C的对边分别为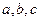 ,向量
,向量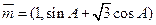 ,
,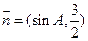 ,且
,且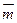 与
与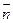 共线。
共线。
(1)求角A的大小;
(2)若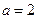 ,
,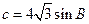 ,且△ABC的面积小于
,且△ABC的面积小于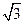 ,求角B的取值范围。
,求角B的取值范围。
(本小题9分)等差数列{an}不是常数列,a5=10,且a5,a7,a10是某一等比数列{bn}的第1,2,3项,(1)求数列{an}的第20项,(2)求数列{bn}的通项公式。