【课本节选】
反比例函数y=(k为常数,k≠0)的图象是双曲线.当k>0时,双曲线两个分支分别在三象限,在每一个象限内,y随x的增大而减小(简称增减性);反比例函数的图象关于原点对称(简称对称性).这些我们熟悉的性质,可以通过说理得到吗?
【尝试说理】
我们首先对反比例函数y=(k>0)的增减性来进行说理.如图,当x>0时.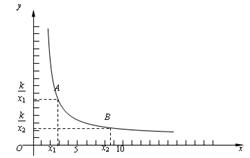
在函数图象上任意取两点A、B,设A(x1,),B(x2,),
且0<x1<x2.
下面只需要比较和的大小.
—=.
∵0<x1<x2,∴x1-x2<0,x1 x2>0,且 k>0.
∴<0.即<.
这说明:x1<x2时,>.也就是:自变量值增大了,对应的函数值反而变小了.
即:当x>0时,y随x的增大而减小.
同理,当x<0时,y随x的增大而减小.
(1)试说明:反比例函数y= (k>0)的图象关于原点对称.
【运用推广】
(2)分别写出二次函数y=ax2(a>0,a为常数)的对称性和增减性,并进行说理.
对称性: ;
增减性: .
说理:
(3)对于二次函数y=ax2+bx+c (a>0,a,b,c为常数),请你从增减性的角度,简要解释为何当x=—时函数取得最小值.
请你按下列程序进行计算,把答案填写在表格内,然后看看有什么规律,想想为什么会有这样的规律?
填写表内的空格:

你发现的规律是:
请说明你发现的规律
计算



如图,AB∥CD,P是直线AB和CD之间的一动点,当P运动到某一位置时,连结PA、PC。
当P在运动过程中构成了不同类型的∠APC,试画出各种不同类型的图形;
写出∠APC、∠PAB、∠PCD之间的等量关系;
试证明(2)中的关系之一。
图a是一个长为2 m、宽为2 n的长方形, 沿图中虚线用剪刀均分成四块小长方形, 然后按图b的形状拼成一个正方形

你认为图b中的阴影部分的正方形的边长等于
请用两种不同的方法求图b中阴影部分的面积
观察图b你能写出下列三个代数式之间的等量关系吗?
代数式: 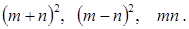
根据(3)题中的等量关系,解决如下问题:若
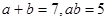 ,求
,求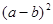 的值
的值
口袋装有编号是1、2、3、4、5的5只形状大小一样的球,其中1、2、3号球是红色,4、5号是白色。规定游戏者一次从口袋中摸出一个球,然后放回第二次再摸一个球,然后再放回。另规定甲再次摸到红球获胜,规定乙摸到一红一白或二白获胜,你认为游戏对双方公平吗?请说明理由。