(本小题满分13分)已知函数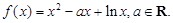
(Ⅰ)若函数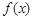 在
在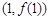 处的切线垂直于
处的切线垂直于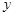 轴,求实数a的值;
轴,求实数a的值;
(Ⅱ)在(Ⅰ)的条件下,求函数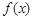 的单调区间;
的单调区间;
(Ⅲ)若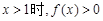 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
在直角坐标系
中,以坐标原点为极点,
轴为极轴建立极坐标系,半圆
的极坐标方程为
,
.
(1)求
的参数方程;
(2)设点 在 上, 在 处的切线与直线 垂直,根据(1)中你得到的参数方程,确定 的坐标.
如图, 是 外一点, 是切线, 为切点,割线 与 相交于点 , , 为 的中点, 的延长线交 于点 .

证明:(1)
;
(2)
已知函数
.
(1)讨论
的单调性;
(2)设
,当
时,
,求
的最大值;
(3)已知
,估计
的近似值(精确到0.001).
设
分别是椭圆
的左右焦点,
是
上一点且
与
轴垂直,直线
与
的另一个交点为
.
(1)若直线
的斜率为
,求
的离心率;
(2)若直线
在
轴上的截距为2,且
,求
.
某地区2007年至2013年农村居民家庭纯收入
(单位:千元)的数据如下表:
| 年份 |
2007 |
2008 |
2009 |
2010 |
2011 |
2012 |
2013 |
| 年份代号 | 1 |
2 |
3 |
4 |
5 |
6 |
7 |
| 人均纯收入 | 2.9 |
3.3 |
3.6 |
4.4 |
4.8 |
5.2 |
5.9 |
(1)求
关于
的线性回归方程;
(2)利用(1)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘法估计公式分别为: ,
,