我们已经学过将一个多项式分解因式的方法有提公因式法和运用公式法,其实分解因式的方法还有分组分解法、拆项法、十字相乘法等等。
(1)分组分解法:将一个多项式适当分组后,可提公因式或运用公式继续分解的方法。
如:

(2)拆项法:将一个多项式的某一项拆成两项后,可提公因式或运用公式继续分解的方法。如:
请你仿照以上方法,探索并解决下列问题:
<1>分解因式: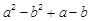 ;
;
<2>分解因式: ;
;
<3>分解因式: .
.
(1)解方程:4x2-8x-3=0
(2)求抛物线 与x轴和y轴的交点坐标.
与x轴和y轴的交点坐标.
已知:如图,线段a.求作:正方形ABCD,使正方形ABCD的对角线AC=a.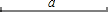
已知两个多项式分别用 表示,计算
表示,计算 .某同学做此题时误将
.某同学做此题时误将 看成了
看成了 ,求得其结果为
,求得其结果为 =
= ,若
,若 ,请你帮助他求得正确答案.
,请你帮助他求得正确答案.
某检修小组乘一辆检修车沿铁路检修,规定向东走为正,向西走为负,小组的出发地记为0,某天检修完毕时,行走记录(单位:千米)如下:
10,-2,+3,-1,+9,-3,-2,+11,+3,-4,+6.
(1)问收工时,检修小组距出发地有多远?在东侧还是西侧?
(2)若检修车每千米耗油0.8升,求从出发到收工共耗油多少升?
用式子表示十位上的数是 ,个位上的数是
,个位上的数是 的两位数,再把这个两位数的十位上的数与个位上的数交换位置,计算所得数与原数的和.
的两位数,再把这个两位数的十位上的数与个位上的数交换位置,计算所得数与原数的和.