各项为正的数列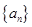 满足
满足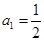 ,
,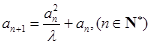 ,
,
(1)取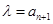 ,求证:数列
,求证:数列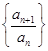 是等比数列,并求其公比;
是等比数列,并求其公比;
(2)取 时,令
时,令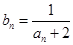 ,记数列
,记数列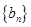 的前
的前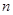 项和为
项和为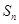 ,数列
,数列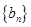 的前
的前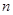 项之积为
项之积为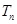 ,求证:对任意正整数
,求证:对任意正整数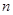 ,
,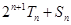 为定值.
为定值.
已知 , 且
, 且 ,求证:
,求证: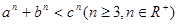
(本小题满分10分)
已知圆O: ,圆C:
,圆C: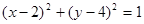 ,由两圆外一点
,由两圆外一点 引两圆切线PA、PB,切点分别为A、B,满足|PA|=|PB|.
引两圆切线PA、PB,切点分别为A、B,满足|PA|=|PB|.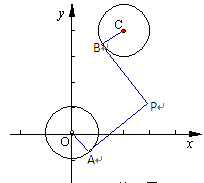
(Ⅰ)求实数a、b间满足的等量关系;
(Ⅱ)求切线长|PA|的最小值;
(Ⅲ)是否存在以P为圆心的圆,使它与圆O相内切并且与圆C相外切?若存在,求出圆P的方程;若不存在,说明理由.
(本小题满分10分)
已知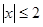 ,
,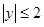 ,点
,点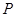 的坐标为
的坐标为
(1)当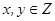 时,求
时,求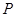 的坐标满足
的坐标满足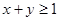 的概率。
的概率。
(2)当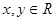 时,求
时,求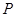 的坐标满足
的坐标满足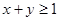 的概率。
的概率。
(本小题满分10分)
用秦九韶算法演算出多项式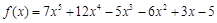 在
在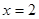 时的值.
时的值.
(必须写出相应的完整步骤,只写答案不给分,缺少相应步骤将扣除相应的步骤分)
(本题共两个小题,每题5分,满分10分)
① 已知不等式 的解集是
的解集是 ,求
,求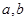 的值;
的值;
② 若函数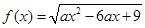 的定义域为
的定义域为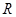 ,求实数
,求实数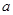 的取值范围.
的取值范围.