“中国竹乡”安吉县有着丰富的毛竹资源.某企业已收购毛竹52.5吨,根据市场信息,如将毛
竹直接销售,每吨可获利l00元;如果对毛竹进行粗加工,每天可加工8吨。每吨可获利1000元;如果进
行精加工,每天可加工0.5吨,每吨可获利5000元.由于受条件限制.在同一天中只能采用一种方式加工,
并且必须在一个月(30天)内将这批毛竹全部销售,为此研究了两种方案:
(1) 方案一:将毛竹全部粗加工后销售,则可获利 元.
(2)方案二:30天时间都进行精加工,未来得及加工的毛竹,在市场上直接销售,则可获利 .
(3)问:是否存在第三种方案,将部分毛竹精加工.其余毛竹粗加工,并且恰好在30天内完成?若存在,求销售后所获利润,若不存在,请说明理由.
(1)如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.求证:CE=CF;
(2)如图2,在正方形ABCD中,E是AB上一点,G是AD上一点,如果∠GCE=45°,请你利用(1)的结论证明:GE=BE+GD.
(3)运用(1)(2)解答中所积累的经验和知识,完成下题:
如图3,在直角梯形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC,E是AB上一点,且∠DCE=45°,BE=4,DE=10,求直角梯形ABCD的面积.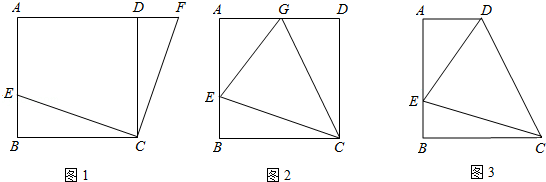
有两块面积相同的试验田,分别收获蔬菜900kg和1500kg,已知第一块试验田每亩收获蔬菜比第二块少300kg,求第一块试验田每亩收获蔬菜多少千克?
已知:Rt△ABC中,∠C=90°,∠CAB的平分线与外角∠CBE的平分线相交于点D.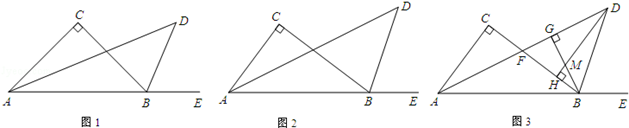
(1)如图1,若CA=CB,则∠D= 度;
(2)如图2,若CA≠CB,求∠D的度数;
(3)如图3,在(2)的条件下,AD与BC相交于点F,过B作BG⊥DF,过D作DH⊥BF,垂足分别为G,H,BG,DH相交于点M.若FG=2,DG=4,求BH的长.
如图,在▱ABCD中,E、F分别为边ABCD的中点,BD是对角线,过A点作平行四边形AGDB交CB的延长线于点G.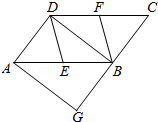
(1)求证:DE∥BF;
(2)若∠G=90,求证:四边形DEBF是菱形.
如图,将▱ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.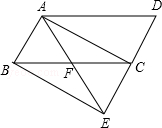
(1)求证:△ABF≌△ECF;
(2)若∠AFC=2∠D,连接AC、BE,求证:四边形ABEC是矩形.