解方程：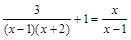
.
有20筐白菜，以每筐25千克为标准，超过或不足的分别用正、负来表示，记录如下：
| 与标准质量的差（单位：千克） |
－3 |
－2 |
－1.5 |
0 |
1 |
2.5 |
| 筐数 |
1 |
4 |
2 |
3 |
2 |
8 |
（1）与标准质量比较，20筐白菜总计超过或不足多少千克？
（2）若白菜每千克售价2.6元，则出售这20筐白菜可卖多少元？
化简求值：已知
，求代数式
的值.
将以下有理数：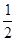
，|-2.5|，0，-22，-（+2），表示在数轴上，并用“<”将它们连接起来.
将
，
，
，
，
，
，
按要求分别填入相应的集合中.
（1）负数集合： ｛……｝;
（2）非负数集合：｛……｝;
（3）有理数集合：｛……｝
如图（1），将两块直角三角尺的直角顶点C叠放在一起，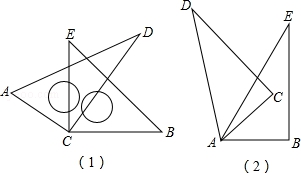
（1）若∠DCE=25°，∠ACB=；若∠ACB=150°，则∠DCE=；
（2）猜想∠ACB与∠DCE的大小有何特殊关系，并说明理由；
（3）如图（2），若是两个同样的直角三角尺60°锐角的顶点A重合在一起，则∠DAB与∠CAE的大小又有何关系，请说明理由．