如图是一把绸扇,线段AD、BC所在的直线相交于点O,弧AB与弧CD是以点O为圆心、半径分别为10cm,20cm的圆弧,且∠AOB=150°,这把绸扇的绸布部分ADCB的面积是多少?(不考虑绸布的折皱,结果用含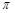
的式子表示)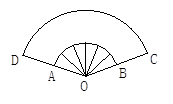
已知,一条弧长为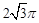
cm,它所对的圆心角为120°,求这条弧所对的弦长.
如图,一个图形由大小相等的五个圆⊙O1、⊙O2、⊙O3、⊙O4和⊙O5构成,其中⊙O1、⊙O2、⊙O3都与直线L相切,并且⊙O1与⊙O2,⊙O2与⊙O3,⊙O3与⊙O4, ⊙O4与⊙O5,⊙O5与⊙O2分别外切.请画一条直线,使得这条直线把图形的面积二等分.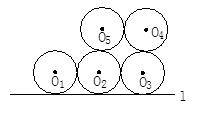
如图,⊙O1、⊙O2交于A、B两点,点O1在⊙O2上,两圆的连心线交⊙O1于E、D,交⊙O2于F,交AB于C,请根据图中所给的已知条件(不再标注其他字母, 不再添加任何辅助线),写出两个线段之间的关系式.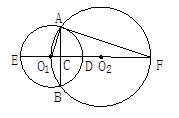
试用10个圆设计一个使各圆都内切的图案.
，并在数轴上表示解集．