解方程组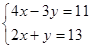
先化简,再求值:(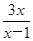 -
-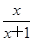 )·
)·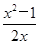 ,其中x=-3.
,其中x=-3.
(本小题满分12分)如图,平面直角坐标系中,抛物线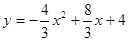 交
交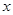 轴于A、B两点(点B在点A的右侧),交
轴于A、B两点(点B在点A的右侧),交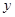 轴于点C,以OC、OB为两边作矩形OBDC,CD交抛物线于G.
轴于点C,以OC、OB为两边作矩形OBDC,CD交抛物线于G.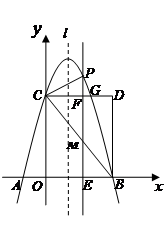
(1)求OC和OB的长;
(2)抛物线的对称轴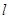 在边OB(不包括O、B两点)上作平行移动,交
在边OB(不包括O、B两点)上作平行移动,交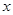 轴于点E,交CD于点F,交BC于点M,交抛物线于点P.设OE=m,PM=h,求h与m的函数关系式,并求出PM的最大值;
轴于点E,交CD于点F,交BC于点M,交抛物线于点P.设OE=m,PM=h,求h与m的函数关系式,并求出PM的最大值;
(3)在(2)的情况下,连接PC,则在CD上方的抛物线部分是否存在这样的点P,使得以P、C、F为顶点的三角形和△BEM相似?若存在,直接写出此时m的值,并直接判断此时△PCM的形状;若不存在,请说明理由.
(本题12分)某学校活动小组在作三角形的拓展图形,研究其性质时,经历了如下过程:
(1)●操作发现:
在等腰△ABC中,AB=AC,分别以AB和AC为斜边,向△ABC的外侧作等腰直角三角形,如图1所示,其中DF⊥AB于点F,EG⊥AC于点G,M是BC的中点,连接MD和ME,则下列结论正确的是①②③④
(填序号即可)
①AF=AG=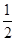 AB;②MD=ME;③整个图形是轴对称图形.
AB;②MD=ME;③整个图形是轴对称图形.
(2)●数学思考:
在任意△ABC中,分别以AB和AC为斜边,向△ABC的外侧作等腰直角三角形,如图2所示,M是BC的中点,连接MD和ME,则MD与ME具有怎样的数量和位置关系?请给出证明过程;
(3)●类比探究:
在任意△ABC中,仍分别以AB和AC为斜边,向△ABC的内侧作等腰直角三角形,如图3所示,M是BC的中点,连接MD和ME,则△MED的形状为___________________.等腰直角三角形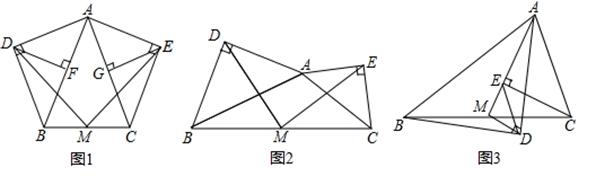
(本题10分)黄岩岛是我国南沙群岛的一个小岛,渔产丰富.一天某渔船离开港口前往该海域捕鱼.捕捞一段时间后,发现一外国舰艇进入我国水域向黄岩岛驶来,渔船向渔政部门报告,并立即返航.渔政船接到报告后,立即从该港口出发赶往黄岩岛.下图是渔政船及渔船与港口的距离s和渔船离开港口的时间t之间的函数图象.(假设渔船与渔政船沿同一航线航行)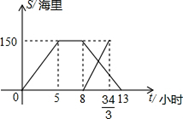
(1)直接写出渔船与港口的距离s和渔船离开港口的时间t之间的函数关系式
(2)求渔船与渔政船相遇时,渔船与黄岩岛的距离.
(3在渔政船驶往黄岩岛的过程中,求渔船从港口出发经过多长时间与渔政船相距30海里?