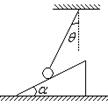
一转动装置如图所示,四根轻杆
、
、
和
与两小球以及一小环通过铰链连接,轻杆长均为l,球和环的质量均为
,
端固定在竖直的轻质转轴上,套在转轴上的轻质弹簧连接在
与小环之间,原长为
,装置静止时,弹簧长为
,转动该装置并缓慢增大转速,小环缓慢上升。弹簧始终在弹性限度内,忽略一切摩擦和空气阻力,重力加速度为
,求

(1)弹簧的劲度系数 ;
(2)AB杆中弹力为零时,装置转动的角速度 ;
(3)弹簧长度从
缓慢缩短为
的过程中,外界对转动装置所做的功
。
加速度计是测定物体加速度的仪器,在现代科技中,它已成为导弹、飞机、潜艇或宇宙飞船制导系统的信息源,如图所示为应变式加速度计,当系统加速时,加速度计中的敏感元件也处于加速状态,敏感元件由弹簧连接并架在光滑支架上,支架与待测系统固定在一起,敏感元件下端滑动臂可在滑动变阻器R上自由滑动,静止时位于滑动变阻器中央,当系统加速时,敏感元件发生位移,并转化成电信号输出。已知敏感元件的质量为m,两侧弹簧的劲度系数为k,电源电动势为E,内阻不计,滑动变阻器的总阻值为R,有效长度为L,静态时输出电压为U0,问如何用输出信号的电压U来表示待测系统的加速度。测量范围是多少?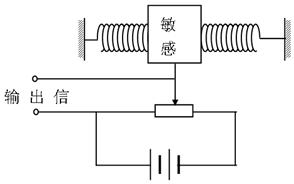
如图示,电流表读数为0.75A,电压表读数为2V,R3=" 4Ω" ,经过一段时间后某一电阻烧断,电流表读数变为0.8A,电压表读数变为3.2V,设电表对电路的影响不计,试问:
(1)烧断的是哪一个电阻?
(2)电源的电动势和内阻分别是多少?
如图所示,电源电动势E=9V,内电阻r=0.5Ω,电阻R1=5.0Ω、R2=3.5Ω、R3=6.0Ω、R4=3.0Ω,电容C="2.0" μF。
求:当电键K由a与接触到与b接触通过R3的电量是多少?
一圆环A套在一均匀圆木棒B上,A的高度相对B的长度来说可以忽略不计。A和B的质量都等于m,A和B之间的滑动摩擦力为f(f < mg)。开始时B竖直放置,下端离地面高度为h,A在B的顶端,如图所示。让它们由静止开始自由下落,当木棒与地面相碰后,木棒以竖直向上的速度反向运动,并且碰撞前后的速度大小相等。设碰撞时间很短,不考虑空气阻力,问:在B再次着地前,要使A不脱离B, B至少应该多长?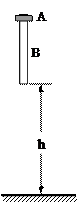
如图所示,小球被轻质细绳系住斜吊着放在静止的光滑斜面上,设小球质量m=1kg,斜面倾角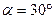 ,悬线与竖直方向夹角
,悬线与竖直方向夹角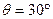 ,光滑斜面的质量为3kg,置于粗糙水平面上.g=10m/s2.
,光滑斜面的质量为3kg,置于粗糙水平面上.g=10m/s2.
求:(1)悬线对小球拉力大小.
(2)地面对斜面的摩擦力的大小和方向.