某批乒乓球的质量检验结果如下:
| 抽取的球数n |
50 |
100 |
200 |
500 |
1000 |
1500 |
2 000 |
| 优等品频数m |
45 |
91 |
179 |
445 |
905 |
1350 |
1800 |
优等品频率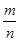 |
0.900 |
0.910 |
|
0.890 |
|
0.900 |
0.900 |
(1)填写表中的空格;
(2)画出这批乒乓球“优等品”频率的折线统计图;
(3)这批乒乓球“优等品”的概率的估计值是多少? 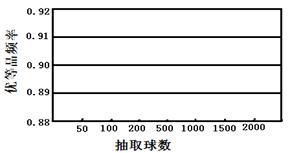
(本题12分)某超市用3000元购进某种干果销售,由于销售状况良好,超市又调拨9000元资金购进该种干果,但这次的进价比第一次的进价提高了20%,购进干果的数量是第一次的2倍还多300千克,如果超市按每千克9元的价格出售,当大部分干果售出后,余下的600千克按售价的8折售完.
(1)该种干果的第一次进价是每千克多少元?
(2)超市销售这种干果共盈利多少元?
(本题10分)准备一张矩形纸片,按如图操作:将△ABE沿BE翻折,使点A落在对角线BD上的M点,将△CDF沿DF翻折,使点C落在对角线BD上的N点.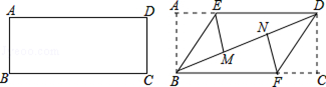
(1)求证:四边形BFDE是平行四边形;
(2)若四边形BFDE是菱形, AB=2,求菱形BFDE的面积.
(本题10分)用你发现的规律解答下列问题.

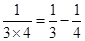 ┅┅
┅┅
(1) 计算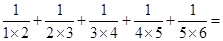 .
.
(2)探究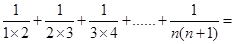 .(用含有
.(用含有 的式子表示)
的式子表示)
(3)若 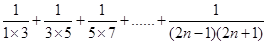 的值为
的值为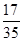 ,求
,求 的值.
的值.
(本题9分)为了了解“通话时长”(“通话时长”指每次通话时间)的分布情况,小强收集了他家1000个“通话时长”数据,这些数据均不超过18(单位:分钟),他从中随机抽取了若干个数据作为样本,统计结果如下表,并绘制了不完成的频数分布直方图.
| “通话时长” x/分钟 |
0<x≤3 |
3<x≤6 |
6<x≤9 |
9<x≤12 |
12<x≤15 |
15<x≤18 |
| 次数 |
36 |
a |
8 |
12 |
8 |
12 |
|
根据图、表提供的信息,解答下列问题:
(1)a= ,样本容量是 ,并将这个频数分布直方图补充完整;
|
(2)求样本中“通话时长”不超过9分钟的频率;
(3)请估计小强家这1000次通话中“通话时长”超过15分钟的次数.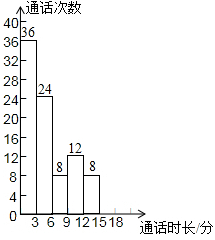
(本题6分)如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图并标好相应的字母: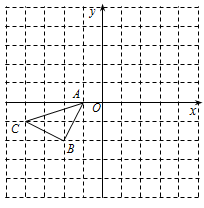
(1)以A点为旋转中心,将△ABC绕点A顺时针旋转 得△AB1C1,画出△AB1C1.
得△AB1C1,画出△AB1C1.
(2)作出△ABC关于坐标原点O成中心对称的△A2B2C2.