如图,在平面直角坐标系中,顶点为(4,-1)的抛物线交y轴于A点,交x轴于B,C两点(点B在点C的左侧),已知A点坐标为(0,3)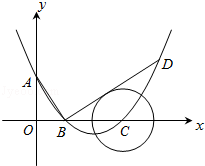
(1)求此抛物线的解析式;
(2)过点B作线段AB的垂线交抛物线于点D,如果以点C为圆心的圆与直线BD相切,请判断抛物线的对称轴l与⊙C有怎样的位置关系,并给出证明;
(3)已知点P是抛物线上的一个动点,且位于A,C两点之间,问:当点P运动到什么位置时,△PAC的面积最大?并求出此时P点的坐标和△PAC的最大面积.
如图是按一定规律排列的方程组集合和它解的集合的对应关系图,若方程组从左至右依次记作方程组1、方程组2、方程组3、……方程组n.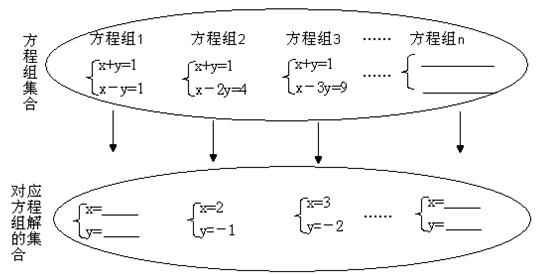
⑴将方程组1的解填入图中;
⑵请依据方程组和它的解的变化规律,将方程组n和它的解直接填入集合图中;
⑶若方程组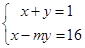 的解是
的解是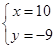 ,求
,求 的值,并判断该方程组是否符合(2)中的规律?
的值,并判断该方程组是否符合(2)中的规律?
学生会准备调查全校七年级学生每天(除课间操外)的课外锻炼时间.
⑴ 确定调查方式时,甲同学说:“我到1班去调查全体同学”;乙同学说:“我到体育场上去询问参加锻炼的同学”;丙同学说:“我到全校七年级每个班去随机调查一定数量的同学”.你认为调查方式最为合理的是(填“甲”或“乙”或“丙”);
⑵ 他们采用了最为合理的调查方法收集数据,并绘制出如图1所示的条形统计图和如图2所示的扇形统计图,请将两幅统计图补充完整;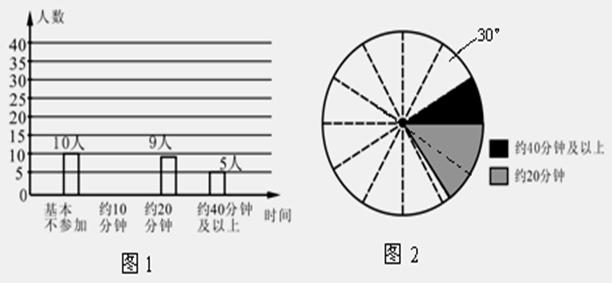
⑶ 若该校七年级共有1200名同学,请你估计其中每天(除课间操外)课外锻炼时间不大于20分钟的人数,并根据调查情况向学生会提出一条建议.(注:图2中相邻两虚线形成的圆心角为30°)
将某雷达测速区监测到的一组汽车的时速数据整理,得到其频数及频率如下表(未完成):
| 数据段 |
30~40 |
40~50 |
50~60 |
60~70 |
70~80 |
总计 |
| 频数 |
10 |
36 |
20 |
|||
| 频率 |
0.05 |
0.39 |
0.10 |
1 |
注:30~40为时速大于等于30千米而小于40千米,其他类同.
(1)请你把表中的数据填写完整;
(2)补全频数分布直方图;
(3)如果此路段汽车时速超过60千米即为违章,
则违章车辆共有多少辆.
解不等式组,并把解集在数轴上表示出来: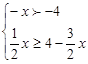
如图,∠1=∠2,∠3=∠4,∠A=1100,求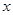 的值。
的值。