如图,在平面直角坐标系xOy中,AB在x轴上,以AB为直径的半圆⊙O‘与y轴正半轴交于点C,连接BC,AC.CD是半圆⊙O’的切线,AD⊥CD于点D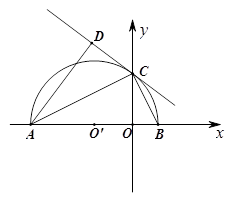
(1)求证:∠CAD =∠CAB
(2)已知抛物线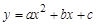 过A、B、C三点,AB=10,tan∠CAD=
过A、B、C三点,AB=10,tan∠CAD=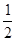 .
.
① 求抛物线的解析式
② 判断抛物线的顶点E是否在直线CD上,并说明理由;
③ 在抛物线上是否存在一点P,使四边形PBCA是直角梯形.若存在,直接写出点P的坐标(不写求解过程);若不存在,请说明理由.
下面的计算对不对?如果不对,应怎样改正?
(1)3a2·4a3=7a5;(2)2x3·3x4=5x12;(3)3m2·(-5m2)=-15m2.
已知⊙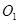 与⊙
与⊙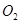 相交于
相交于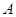 、
、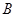 两点,点
两点,点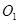 在⊙
在⊙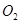 上,
上, 为⊙
为⊙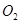 上一点(不与
上一点(不与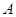 ,
,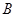 ,
,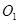 重合),直线
重合),直线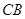 与⊙
与⊙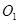 交于另一点
交于另一点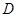 。
。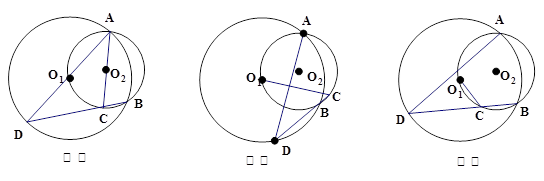
(1)如图(1),若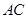 是⊙
是⊙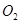 的直径,求证:
的直径,求证: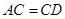 ;
;
(2)如图(2),若 是⊙
是⊙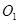 外一点,求证:
外一点,求证: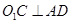 ;
;
(3)如图(3),若 是⊙
是⊙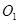 内一点,判断(2)中的结论是否成立。
内一点,判断(2)中的结论是否成立。
有两个全等的等腰直角三角板ABC和EFG其直角边长均为6(如图1所示)叠放在一起,使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合.现将三角板EFG绕O点顺时针旋转,旋转角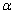 满足0<º
满足0<º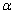 <90º,四边形CHGK是旋转过程中两块三角板的重叠部分(如图2).
<90º,四边形CHGK是旋转过程中两块三角板的重叠部分(如图2).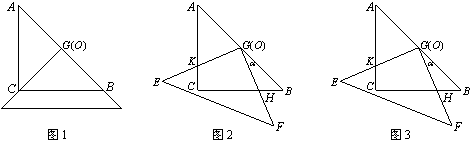
(1)在上述旋转过程中,①BH与CK有怎样的数量关系?②四边形CHGK的面积是否发生变化?并证明你发现的结论.
(2)如图,连接KH,在上述旋转过程中,是否存在某一位置使△GKH的面积恰好等于△ABC面积的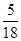 ?若存在,请求出此时KC的长度;若不存在,请说明理由.
?若存在,请求出此时KC的长度;若不存在,请说明理由.
仙游永辉超市经销度尾文旦柚,如果每千克盈利10元,每天可售出500千克,经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量减少20千克,现该超市要保证每天盈利6000元,同时又要使顾客最实惠,那么每千克应涨价多少元?
如图,C是射线OE上的一动点,AB是过点C的弦,直线DA与OE的交点为D,现有三个论断: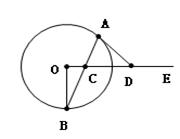
(1)DA是⊙O的切线;(2)DA=DC;(3)OD⊥OB。
请以其中两个为条件,另一个为结论,写出一个真命题,用“○○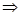 ○”表示。并证明。
○”表示。并证明。
我的是:。