(本小题满分7分)选修4—2:矩阵与变换
在平面直角坐标系中,矩阵 对应的变换将平面上任意一点
对应的变换将平面上任意一点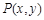 变换为点
变换为点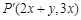 .
.
(1)求矩阵 的逆矩阵
的逆矩阵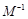 ;
;
(2)求曲线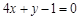 在矩阵
在矩阵 的变换作用后得到的曲线
的变换作用后得到的曲线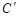 的方程.
的方程.
解关于 的不等式:
的不等式: .
.
如图,射线 、
、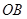 所在的直线的方向向量分别为
所在的直线的方向向量分别为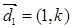 、
、 (
(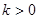 ),点
),点 在
在 内,
内, 于
于 ,
,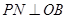 于
于 .
.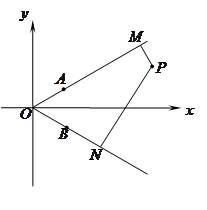
(1)若 ,
,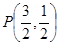 ,求
,求 的值;
的值;
(2)若 ,△
,△ 的面积为
的面积为 ,求
,求 的值;
的值;
(3)已知 为常数,
为常数, 、
、 的中点为
的中点为 ,且
,且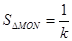 ,当
,当 变化时,求
变化时,求 的取值范围.
的取值范围.
已知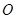 为
为 的外心,以线段
的外心,以线段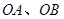 为邻边作平行四边形,第四个顶点为
为邻边作平行四边形,第四个顶点为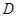 ,再以
,再以 为邻边作平行四边形,它的第四个顶点为
为邻边作平行四边形,它的第四个顶点为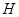 .
.
(1) 若 ,试用
,试用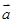 、
、 、
、 表示
表示 ;
;
(2) 证明: ;
;
(3) 若 的
的 ,
, ,外接圆的半径为
,外接圆的半径为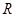 ,用
,用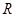 表示
表示 .
.
在直角坐标系中,已知两点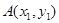 ,
,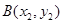 ;
;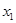 ,
,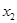 是一元二次方程
是一元二次方程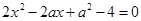 两个不等实根,且
两个不等实根,且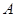 、
、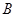 两点都在直线
两点都在直线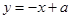 上.
上.
(1)求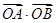 ;
;
(2) 为何值时
为何值时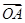 与
与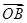 夹角为
夹角为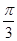 .
.
已知 的顶点
的顶点 ,
, 边上的中线所在的直线方程是
边上的中线所在的直线方程是 ,AC边上的高所在的直线方程是
,AC边上的高所在的直线方程是 .
.
求:(1)AC边所在的直线方程;
(2)AB边所在的直线方程.