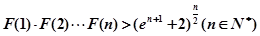(本题满分14分,第(1)、(2)小题各3分;第(3)、(4)小题各4分)
请你指出函数
 的基本性质(不必证明),并判断以下四个命题的正确性,必要时可直接运用有关其基本性质的结论加以证明.
的基本性质(不必证明),并判断以下四个命题的正确性,必要时可直接运用有关其基本性质的结论加以证明.
(1)当 时,等式
时,等式 恒成立;
恒成立;
(2)若 ,则一定有
,则一定有 ;
;
(3)若 ,方程
,方程 有两个不相等的实数解;
有两个不相等的实数解;
(4)函数 在
在 上有三个零点.
上有三个零点.
已知函数 .
.
(Ⅰ)若函数 在
在 上是增函数,求正实数
上是增函数,求正实数 的取值范围;
的取值范围;
(Ⅱ)当 时,求函数
时,求函数 在
在 上的最大值和最小值;
上的最大值和最小值;
已知函数
(1)求数列{an}的通项an;
(2)若数列{bn}的前n项和 求Tn.
求Tn.
某人居住在城镇的 处,准备开车到单位
处,准备开车到单位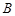 处上班,若该地各路段发生堵车事件都是相互独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率如图(例如
处上班,若该地各路段发生堵车事件都是相互独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率如图(例如 算作两个路段:路段
算作两个路段:路段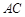 发生堵车事件的概率为
发生堵车事件的概率为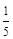 ,路段
,路段 发生堵车事件的概率为
发生堵车事件的概率为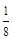 ).
).
(Ⅰ)请你为其选择一条由 到
到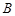 的最短路线(即此人只选择从西向东和从南向北的路线),使得途中发生堵车事件的概率最小;
的最短路线(即此人只选择从西向东和从南向北的路线),使得途中发生堵车事件的概率最小;
(Ⅱ)若记路线 中遇到堵车次数为随机变量
中遇到堵车次数为随机变量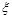 ,求
,求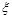 的数学期望
的数学期望 .
.
(Ⅰ)在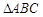 中,若
中,若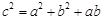 ,求角
,求角 的大小.
的大小.
(Ⅱ)对于(Ⅰ)中的角 ,函数
,函数 的图象按向量
的图象按向量 平移后,对应的函数为偶函数,求
平移后,对应的函数为偶函数,求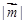 取最小值时的向量
取最小值时的向量 .
.
已知函数
(1)若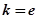 ,试确定函数
,试确定函数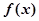 的单调区间;
的单调区间;
(2)若 且对任意
且对任意 ,
,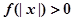 恒成立,试确定实数
恒成立,试确定实数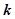 的取值范围;
的取值范围;
(3)设函数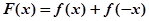 ,求证:
,求证: