已知抛物线y＝ax2－2ax＋c与y轴交于C点，与x轴交于A、B两点，点A的坐标是（-1,0），O是坐标原点，且OC=3OA．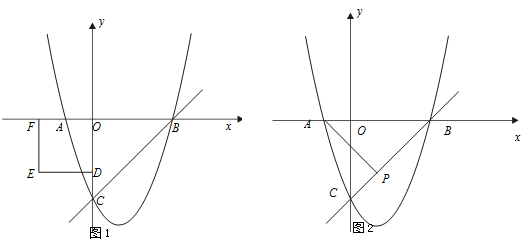
（1）求抛物线的函数表达式；
（2）直接写出直线BC的函数表达式；
（3）如图1，D为y轴的负半轴上的一点，且OD=2，以OD为边作正方形ODEF．将正方形ODEF以每秒1个单位的速度沿x轴的正方向移动，在运动过程中，设正方形ODEF与△OBC重叠部分的面积为s，运动的时间为t秒（0＜t≤2）．
求：①s与t之间的函数关系式；
②在运动过程中，s是否存在最大值？如果存在，直接写出这个最大值；如果不存在，请说明理由．
（4）如图2，点P（1，k）在直线BC上，点M在x轴上，点N在抛物线上，是否存在以A、M、N、P为顶点的平行四边形？若存在，请直接写出M点坐标；若不存在，请说明理由．
已知△ABC是等边三角形，D是BC边上的一个动点（点D不与B，C重合）△ADF是以AD为边的等边三角形，过点F作BC的平行线交射线AC于点E，连接BF．
（1）如图1，求证：△AFB≌△ADC；
（2）请判断图1中四边形BCEF的形状，并说明理由；
（3）若D点在BC 边的延长线上，如图2，其它条件不变，请问（2）中结论还成立吗？如果成立，请说明理由．
如图，△ABC是等腰直角三角形，延长BC至E使BE=BA，过点B作BD⊥AE于点D，BD与AC交于点F，连接EF．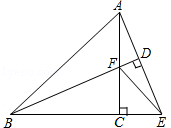
（1）求证：BF=2AD；
（2）若CE=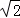
，求AC的长．
某文具店第一次用400元购进胶皮笔记本若干个，第二次又用400元购进该种型号的笔记本，但这次每个的进价是第一次进价的1.25倍，购进数量比第一次少了20个．
（1）求第一次每个笔记本的进价是多少？
（2）若要求这两次购进的笔记本按同一价格全部销售完毕后后获利不低于460元，问每个笔记本至少是多少元？
如图所示，已知△ABC的三个顶点的坐标分别为A（﹣2，3），B（﹣6，0），C（﹣1，0）．
（1）请直接写出点B关于点A对称的点的坐标；
（2）将△ABC绕坐标原点O逆时针旋转90°，画出图形，直接写出点B的对应点的坐标；
（3）请直接写出：以A、B、C为顶点的平行四边形的第四个顶点D的坐标．
如图，在▱ABCD中，点E是BC边的中点，连接AE并延长与DC的延长线交于F．
（1）求证：CF=CD；
（2）若AF平分∠BAD，连接DE，试判断DE与AF的位置关系，并说明理由．