(本小题满分14分)已知数列{an}的前n项和为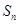 ,且满足
,且满足 ,数列
,数列 满足
满足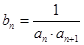 ,
,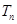 为数列
为数列 的前n项和.
的前n项和.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若对任意的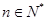 ,不等式
,不等式 恒成立,求实数
恒成立,求实数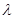 的取值范围;
的取值范围;
(Ⅲ)是否存在正整数m,n(1<m<n),使得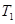 ,
, ,
,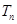 成等比数列?若存在,求出所有m,n的值;若不存在,请说明理由.
成等比数列?若存在,求出所有m,n的值;若不存在,请说明理由.
已知函数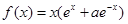 ,
,
(1)当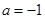 时,判断并证明
时,判断并证明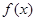 的奇偶性;
的奇偶性;
(2)是否存在实数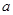 ,使得
,使得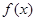 是奇函数?若存在,求出
是奇函数?若存在,求出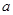 ;若不存在,说明理由。
;若不存在,说明理由。
已知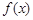 是定义在
是定义在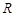 上的奇函数,且当
上的奇函数,且当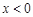 时,
时, .
.
(Ⅰ)求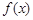 的表达式;
的表达式;
(Ⅱ)判断并证明函数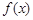 在区间
在区间 上的单调性.
上的单调性.
把长为10cm的细铁丝截成两段,各自围成一个正方形,求这两个正方形面积之和的最小值。
已知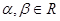 且
且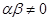 ,数列
,数列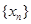 满足
满足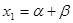 ,
,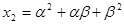 ,
,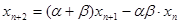 (
(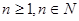 ),令
),令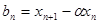 ,
,
⑴求证: 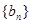 是等比数列;
是等比数列;
⑵求数列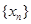 的通项公式;
的通项公式;
⑶若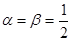 ,求
,求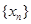 的前
的前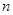 项和
项和 .
.
某投资公司投资甲、乙两个项目所获得的利润分别是P(亿元)和Q亿元),它们与投资额t(亿元)的关系有经验公式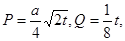 其中
其中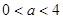 ,今该公司将5亿元投资这两个项目,其中对甲项目投资x(亿元),投资这两个项目所获得的总利润为y(亿元),
,今该公司将5亿元投资这两个项目,其中对甲项目投资x(亿元),投资这两个项目所获得的总利润为y(亿元),
(1)求y关于x的解析式,
(2)怎样投资才能使总利润最大,最大值为多少?.