如图(a)两相距 的平行金属导轨固定于水平面上,导轨左端与阻值 的电阻连接,导轨间虚线右侧存在垂直导轨平面的匀强磁场,质量 的金属杆垂直于导轨上,与导轨接触良好,导轨与金属杆的电阻可忽略,杆在水平向右的恒定拉力作用下由静止开始运动,并始终与导轨垂直,其v-t图像如图(b)所示,在 时撤去拉力,同时使磁场随时间变化,从而保持杆中电流为0,求:
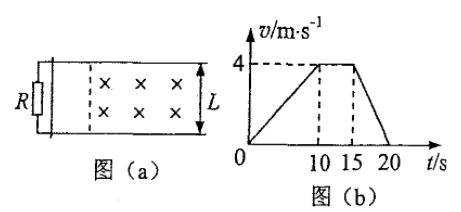
(1)金属杆所受拉力的大小为 ;
(2) 匀强磁场的磁感应强度大小为 ;
(3) 内磁感应强度随时间的变化规律。
汽车紧急刹车后的加速度大小8 m/s2,如果必须使汽车在2s内停下来,那么允许汽车行使的最大速度是多少?如果汽车刹车时速度是20m/s,那么汽车刹车3s时速度是多大?
一物体沿直线运动,先以3m/s的速度运动60m,又以2m/s的速度继续向前运动60m,物体在整个运动过程中平均速度是多少?
一列快车正以60m/s的速度在平直的铁轨上行驶时,发现前面1500m处有一货车正以18m/s的速度匀速同向行驶,快车立即合上制动器,经120s的刹车时间才能停止,试判断两车是否发生撞车事故。
分如图所示,一同学从一高为H=10m高的平台上竖直向上抛出一个可以看成质点的小球,小球的抛出点距离平台的高度为 h0=0.8m,小球抛出后升高了h=0.45m达到最高点,最终小球落在地面上。g="10" m/s2 求: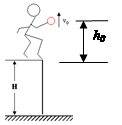
(1)小球抛出时的初速度大小v0
(2)小球从抛出到接触地面的过程中经历的时间t
如图所示,质量为2m的物体A经一轻质弹簧与地面上的质量为3m的物体B相连,弹簧的劲度系数为k,一条不可伸长的轻绳绕过定滑轮,一端连物体A,另一端连一质量为m的物体C,物体A、B、C都处于静止状态.已知重力加速度为g,忽略一切摩擦.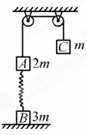
(1)求物体B对地面的压力;
(2)把物体C的质量改为5m,这时C缓慢下降,经过一段时间系统达到新的平衡状态,这时B仍没离开地面,且C只受重力和绳的拉力作用,求此过程中物体A上升的高度.