若函数 是奇函数,则使 成立的 的取值范围为()
| A. | B. | C. | D. |
设f(x)、g(x)分别是定义在R上的奇函数和偶函数,当x<0时,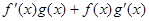 >0.且g(3)=0.则不等式f(x)g(x)<0的解集是 ( )
>0.且g(3)=0.则不等式f(x)g(x)<0的解集是 ( )
| A.(-3,0)∪(3,+∞) | B.(-3,0)∪(0, 3) |
| C.(-∞,- 3)∪(3,+∞) | D.(-∞,- 3)∪(0, 3) |
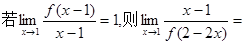 ( )
( )
| A.-1 | B.1 | C.-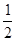 |
D.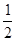 |
设f (x)=∣x-1∣,f
(x)=∣x-1∣,f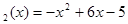 ,函数g(x)是这样定义的:当f
,函数g(x)是这样定义的:当f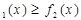 时,g(x)= f
时,g(x)= f (x),当f
(x),当f (x)<f
(x)<f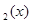 时,g(x)= f
时,g(x)= f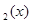 ,若方程g(x)=a有四个不同的实数解,则实数a的取值范围是( )
,若方程g(x)=a有四个不同的实数解,则实数a的取值范围是( )
| A.a<4 | B.0<a<4 | C.0<a<3 | D.3<a<4 |
已知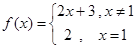 ,下面结论正确的是
,下面结论正确的是
A.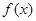 在 在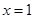 处连续 处连续 |
B.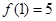 |
C.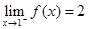 |
D. |
已知数列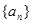 满足
满足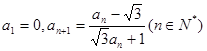 ,则
,则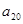 =()
=()
| A. 0 | B.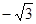 |
C.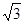 |
D.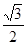 |