设直线l与抛物线 相交于 , 两点,与圆 相切于点 ,且 为线段 的中点.若这样的直线l恰有4条,则 的取值范围是()
| A. | B. | C. | D. |
如图,在矩形 中,
中, ,
, 为线段
为线段 上一动点,现将
上一动点,现将 沿
沿 折起,使点
折起,使点 在面
在面 上的射影
上的射影 在直线
在直线 上,当
上,当 从
从 运动到
运动到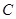 ,则
,则 所形成轨迹的长度为()
所形成轨迹的长度为()
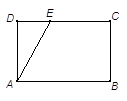
A.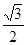 |
B.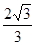 |
C. |
D.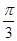 |
已知圆C:(x-3)2+(y-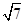 )2=1和两点A(-m,0),B(m,0)(m>0),若圆C上存在点P,使得∠APB=90°,则m的最大值为()
)2=1和两点A(-m,0),B(m,0)(m>0),若圆C上存在点P,使得∠APB=90°,则m的最大值为()
| A.6 | B.5 | C.4 | D.3 |
如图,三棱柱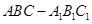 中,侧棱
中,侧棱 垂直底面
垂直底面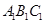 ,底面三角形
,底面三角形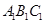 是正三角形,
是正三角形,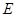 是
是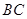 中点,则下列叙述正确的是()
中点,则下列叙述正确的是()
A. 与 与 是异面直线 是异面直线 |
B.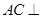 平面 平面 |
C.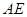 与 与 为异面直线,且 为异面直线,且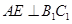 |
D. 平面 平面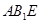 |
在平面直角坐标系内,若曲线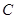 :
: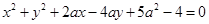 上所有的点均在第二象限内,则实数
上所有的点均在第二象限内,则实数 的取值范围为()
的取值范围为()
A.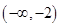 |
B. |
C.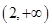 |
D.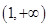 |
在正方体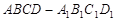 中,
中,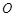 是底面
是底面 的中心,
的中心,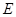 为
为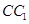 的中点,那么直线
的中点,那么直线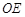 与
与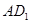 所成角的余弦值为()
所成角的余弦值为()
A.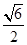 |
B.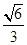 |
C. |
D.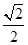 |