如图,在四棱柱 中,侧棱 , ,且点M和N分别为 的中点.

(Ⅰ)求证:
平面
;
(Ⅱ)求二面角
的正弦值;
(Ⅲ)设
为棱
上的点,若直线
和平面
所成角的正弦值为
,求线段
的长
如图,椭圆C: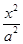 +
+ =1(a>b>0)的焦点F1,F2和短轴的一个端点A构成等边三角形,
=1(a>b>0)的焦点F1,F2和短轴的一个端点A构成等边三角形,
点(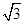 ,
,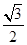 )在椭圆C上,直线l为椭圆C的左准线.
)在椭圆C上,直线l为椭圆C的左准线.
(1) 求椭圆C的方程;
(2) 点P是椭圆C上的动点,PQ ⊥l,垂足为Q.
是否存在点P,使得△F1PQ为等腰三角形?
若存在,求出点P的坐标;若不存在,说明理由.
设有半径为3 的圆形村落,
的圆形村落,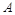 、
、 两人同时从村落中心出发。
两人同时从村落中心出发。 一直向北直行;
一直向北直行;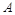 先向东直行,出村后一段时间,改变前进方向,沿着与村落边界相切的直线朝
先向东直行,出村后一段时间,改变前进方向,沿着与村落边界相切的直线朝 所在的方向前进。
所在的方向前进。
(1)若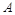 在距离中心5
在距离中心5 的地方改变方向,建立适当坐标系,
的地方改变方向,建立适当坐标系,
求: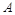 改变方向后前进路径所在直线的方程
改变方向后前进路径所在直线的方程
(2)设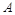 、
、 两人速度一定,其速度比为
两人速度一定,其速度比为 ,且后来
,且后来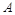 恰与
恰与 相遇.问两人在何处相遇?
相遇.问两人在何处相遇?
(以村落中心为参照,说明方位和距离)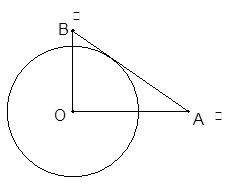
如图,A点在x轴上方,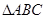 外接圆半径
外接圆半径 ,弦
,弦 在
在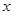 轴上且
轴上且 轴垂直平分
轴垂直平分 边,
边,
(1)求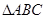 外接圆的标准方程
外接圆的标准方程
(2)求过点 且以
且以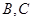 为焦点的椭圆方程
为焦点的椭圆方程
在平行四边形 中,
中,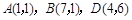 ,点
,点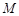 是线段
是线段 的中点,线段
的中点,线段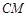 与
与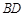 交于点
交于点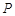 ,
,
(1)求直线 的方程
的方程
(2)求点 的坐标.
的坐标.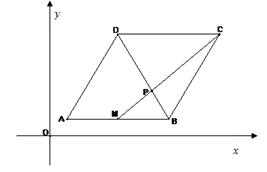
(本小题满分14分)已知函数 =
= ,
,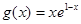 .
.
(1)求函数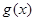 在区间
在区间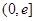 上的值域;
上的值域;
(2)是否存在实数 ,对任意给定的
,对任意给定的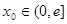 ,在区间
,在区间 上都存在两个不同的
上都存在两个不同的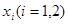 ,使得
,使得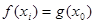 成立.若存在,求出
成立.若存在,求出 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
(3)给出如下定义:对于函数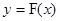 图象上任意不同的两点
图象上任意不同的两点 ,如果对于函数
,如果对于函数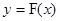 图象上的点
图象上的点 (其中
(其中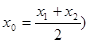 总能使得
总能使得 成立,则称函数具备性质“
成立,则称函数具备性质“ ”,试判断函数
”,试判断函数 是不是具备性质“
是不是具备性质“ ”,并说明理由.
”,并说明理由.