已知x,y均为正数且x+2y=xy,则().
A.xy+ 有最小值4 有最小值4 |
B.xy+ 有最小值3 有最小值3 |
C.x+2y+ 有最小值11 有最小值11 |
D.xy﹣7+ 有最小值11 有最小值11 |
要得到函数y=2sin2x的图象,只需将函数y=2sin(2x﹣ )的图象().
)的图象().
A.向左平移 个单位 个单位 |
B.向右平移 个单位 个单位 |
C.向左平移 个单位 个单位 |
D.向右平移 个单位 个单位 |
若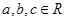 ,且a>b,则下列不等式一定成立的是().
,且a>b,则下列不等式一定成立的是().
| A.a+c≥b﹣c | B.ac>bc |
C.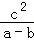 >0 >0 |
D.(a﹣b)c2≥0 |
在等差数列{an}中,若a3+a4+a5+a6+a7=450,则a1+a9的值等于()
| A.45 | B.75 | C.180 | D.300 |
设x、y满足约束条件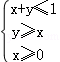 ,则z=2x﹣y的最大值为().
,则z=2x﹣y的最大值为().
| A.0 | B.2 | C.3 | D. |