设 满足约束条件
满足约束条件 ,则下列不等式恒成立的是
,则下列不等式恒成立的是
A.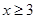 |
B. |
C. |
D. |
已知ABCD是平行四边形,且A(4,1,3),B(2,-5,1),C(3,7,-5),则顶点D的坐标为()
| A.(1,1,-7) | B.(5,3,1) | C.(-3,1,5) | D.(5,13,-3) |
.已知向量 与向量
与向量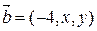 平行,则x,y的值分别是()
平行,则x,y的值分别是()
| A.6和-10 | B.–6和10 | C.–6和-10 | D.6和10 |
如果方程x2+ky2=2表示焦点在y轴上的椭圆,那么实数k的取值范围是()
A. (0,+∞) (0,+∞) |
B.(0,2) | C.(1,+∞) | D.(0,1) |
已知M(-2,0),N(2,0),|PM|-|PN|=4,则动点P的轨迹是()
| A.双曲线 | B.双曲线左支 | C.一条射线 | D.双曲线右支 |
双曲线 的渐近线方程是()
的渐近线方程是()
A. |
B. |
C. |
D. |