如图甲所示，用固定的电动机水平拉着质量m＝2 kg的小物块和质量M＝1 kg的平板以相同的速度一起向右匀速运动，物块位于平板左侧，可视为质点．在平板的右侧一定距离处有台阶阻挡，平板撞上后会立刻停止运动．电动机功率保持P＝3 W不变。从某时刻t＝0起，测得物块的速度随时间的变化关系如图乙所示，t＝6 s后可视为匀速运动，t＝10 s时物块离开木板．重力加速度g＝10 m/s2，求：
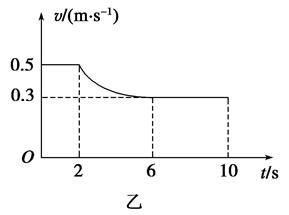
(1)平板与地面间的动摩擦因数μ为多大？
(2)物块在1 s末和3 s末受到的摩擦力各为多大？
(3)平板长度L为多少？
甲车以10 m/s的速度在平直的公路上匀速行驶，乙车以4 m/s的速度与甲车平行同向做匀速直线运动，甲车经过乙车旁边时开始以0.5 m/s2的加速度刹车，从甲车刹车开始计时，求：
(1)乙车在追上甲车前，两车相距的最大距离；
(2)乙车追上甲车所用的时间.
如图所示，一个三棱镜的截面为等腰直角△ABC，∠A为直角.此截面所在平面内的光线沿平行于BC边的方向射到AB边，进入棱镜后直接射到AC边上，并刚好能发生全反射.求该棱镜材料的折射率？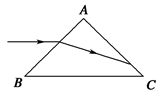
某校一课外活动小组自制一枚火箭，设火箭发射后始终在垂直于地面的方向上运动.火箭点火后可认为做匀加速直线运动，经过4 s到达离地面40 m高处时燃料恰好用完，若不计空气阻力，取g＝10 m/s2，求：
(1)燃料恰好用完时火箭的速度；
(2)火箭上升离地面的最大高度；
把一带电量为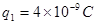
的试探电荷放在电场中的A点，具有
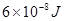的电势能，放在电场中的B点，具有
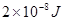的电势能。求：
（1）A、B两点的电势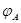
和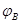
（2）A、B两点间的差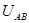
（3）把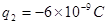
的试探电荷从A点移到B点，电场力对电荷做了多少功？该试探电荷的电势能改变多少？
原子可以从原子间的碰撞中获得能量，从而发生能级跃迁(在碰撞中，动能损失最大的是完全非弹性碰撞)．一个具有13.6 eV动能、处于基态的氢原子与另一个静止的、也处于基态的氢原子发生对心正碰．
(1)是否可以使基态氢原子发生能级跃迁(氢原子能级如图11所示)?
(2)若上述碰撞中可以使基态氢原子发生电离，则氢原子的初动能至少为多少？