小丽为了测旗杆AB的高度,小丽眼睛距地图1.5米,小丽站在C点,测出旗杆A的仰角为30o,小丽向前走了10米到达点E,此时的仰角为60o,求旗杆的高度。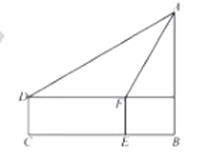
如图,在同一平面上,两块斜边相等的直角三角板Rt△ABC与Rt△ADC拼在一起,使斜边AC完全重合,且顶点B,D分别在AC的两旁,∠ABC=∠ADC=90°,∠CAD=30°,AB=BC=4cm.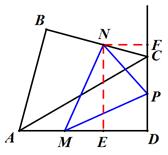
(1)填空:AD= (cm),DC= (cm);
(2)点M,N分别从A点,C点同时以每秒1cm的速度等速出发,且分别在AD,CB上沿A→D,C→B的方向运动,当N点运动 到B点时,M,N两点同时停止运动,连结MN,求当M,N点运动了x秒时,点N到AD的距离(用含x的式子表示);
(3)在(2)的条件下,取DC中点P,连结MP,NP,设△PMN的面积为y(cm2),在整个运动过程中,△PMN的面积y存在最大值,请求出这个最大值.
(参考数据:sin75°=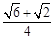 ,sin15°=
,sin15°=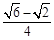 )
)
如图,已知锐角△ABC.
(1)过点A作BC边的垂线MN,交BC于点D(用尺规作图法,保留作图痕迹,不要求写作法);
(2)在(1)条件下,若BC=5,AD=4,tan∠BAD=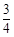 ,求DC的长.
,求DC的长.
某中学初二年级抽取部分学生进行跳绳测试.并规定:每分钟跳90次以下的为不及格;每分钟跳90~99次的为及格;每分钟跳100~109次的为中等;每分钟跳110~119次的为良好;每分钟跳120次及以上的为优秀.测试结果整理绘制成如下两幅不完整的统计图.请根据图中信息,解答下列各题:
(1)参加这次跳绳测试的共有 人;
(2)补全条形统计图;
(3)在扇形统计图中,“中等”部分所对应的圆心角的度数是 ;
(4)如果该校初二年级的总人数是480人,根据此统计数据,请你估算该校初二年级跳绳成绩为“优秀”的人数.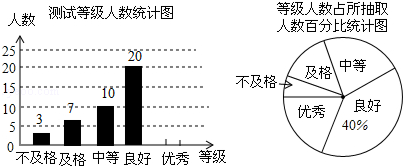
某校体育社团在校内开展“最喜欢的体育项目(四项选一项)”调查,对九年级学生随机抽样,并将收集的数据绘制成如图两幅不完整的统计图,请结合统计图解答下列问题: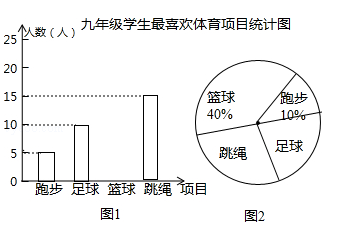
(1)求本次抽样人数有多少人?
(2)补全条形统计图;
(3)该校九年级共有600名学生,估计九年级最喜欢跳绳项目的学生有多少人?