(本题12分)如图,已知直线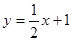 与
与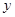 轴交于点
轴交于点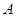 ,与
,与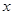 轴交于点
轴交于点 ,抛物线
,抛物线 与直线交于
与直线交于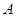 、
、 两点,与
两点,与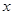 轴交于
轴交于 、
、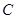 两点,且
两点,且 点坐标为(1,0).
点坐标为(1,0).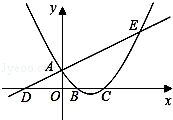
(1)求该抛物线的解析式;
(2)动点 在
在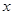 轴上移动,当△
轴上移动,当△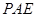 是直角三角形时,直接写出点
是直角三角形时,直接写出点 的坐标;
的坐标;
(3)在抛物线的对称轴上找一点 ,使|
,使|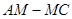 |的值最大,求出点
|的值最大,求出点 的坐标.
的坐标.
已知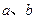 互为相反数,
互为相反数,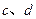 互为倒数,
互为倒数,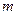 的绝对值为
的绝对值为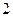 ,求
,求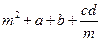 的值.
的值.
计算:⑴
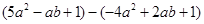
⑵
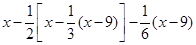
计算:⑴
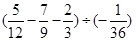
⑵
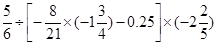
⑶

已知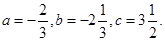
⑴在数轴上标出
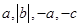 的位置;
的位置;⑵用“<”号把
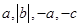 连接起来.
连接起来.
同学们,我们在本期教材的第一章《有理数》中曾经学习过绝对值的概念:一般的,数轴上表示数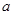 的点与原点的距离叫做数
的点与原点的距离叫做数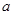 的绝对值,记作
的绝对值,记作 。
。
实际上,数轴上表示数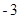 的点与原点的距离科技做
的点与原点的距离科技做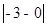 :数轴上表示数
:数轴上表示数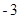 的点与表示数
的点与表示数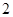 的点的距离可记作
的点的距离可记作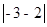 ,那么,
,那么,(I) ①数轴上表示数
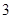 的点与表示数1的点的距离可记作________
的点与表示数1的点的距离可记作________
②数轴上表示数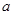 的点与表示数2的点的距离可记作________
的点与表示数2的点的距离可记作________
③数轴上表示数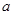 的点与表示数-3的点的距离可记作________
的点与表示数-3的点的距离可记作________(II)数轴上表示到数-2的点的距离为5的点有几个?并求出它们表示的数。
(III)根据(I)中②、③两小题你所填写的结论,请同学们利用数轴探究这两段距离之和的最小值,并简述你的思考过程。