小明、小军两同学做游戏,游戏规则是:一个不透明的文具袋中,装有型号完全相同的3支红笔和2支黑笔,两人先后从袋中取出一支笔(不放回),若两人所取笔的颜色相同,则小明胜,否则,小军胜.
(1)请用树形图或列表法列出摸笔游戏所有可能的结果;
(2)请计算小明获胜的概率,并指出本游戏规则是否公平,若不公平,你认为对谁有利.
如图是七年级(3)班部分学生的座次表,你能用有序数对表示这些同学的座位情况吗?试试看.
如图,在Rt△ABC中,∠B=90°,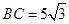 ,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.
,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,请说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.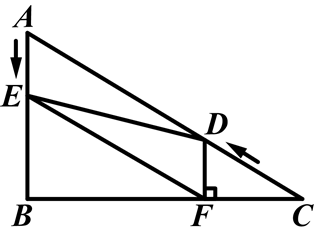
某校九年级学习小组在探究学习过程中,用两块完全相同的且含60°角的直角三角板ABC与AFE按如图(1)所示位置放置,现将Rt△AEF绕A点按逆时针方向旋转角α(0°<α<90°),如图(2),AE与BC交于点M,AC与EF交于点N,BC与EF交于点P.
(1)求证:AM=AN.
(2)当旋转角α=30°时,四边形ABPF是什么样的特殊四边形?并说明理由.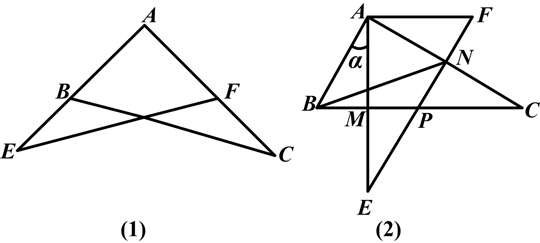
如图中图(1),在正方形ABCD中,E、F分别是边AD、DC上的点,且AF⊥BE.
(1)求证:AF=BE.
(2)如图中图(2),在正方形ABCD中,M、N、P、Q分别是边AB、BC、CD、DA上的点,且MP⊥NQ.MP与NQ是否相等?并说明理由.
如图,将矩形ABCD中的△AOB沿着BC的方向平移线段AD长的距离.
(1)画出△AOB平移后的图形.
(2)设(1)中O点平移后的对应点为E,试判断四边形CODE的形状,并说明理由.
(3)当四边形ABCD是什么四边形时,(2)中的四边形CODE是正方形?并说明你的理由.