(本小题满分12分)已知函数 .
.
(1)若函数 的图象在
的图象在 处的切线斜率为2,求函数
处的切线斜率为2,求函数 的图象在
的图象在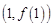 的切线方程;
的切线方程;
(2)若函数 在
在 上是减函数,求实数a的取值范围.
上是减函数,求实数a的取值范围.
如图所示,矩形ABCD中,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE.
(1)求证:AE⊥平面BCE;
(2)求证:AE∥平面BFD;
(3)求三棱锥C-BGF的体积.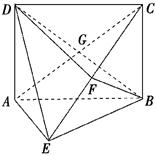
已知正三棱柱ABC—A1B1C1,底面边长AB=2,AB1⊥BC1,点O、O1分别是边AC,A1C1的中点,建立如图所示的空间直角坐标系.
⑴求正三棱柱的侧棱长.
⑵若M为BC1的中点,试用基向量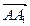 、
、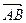 、
、 表示向量
表示向量 ;
;
⑶求异面直线AB1与BC所成角的余弦值.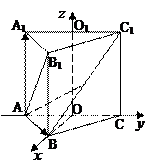
养路处建造圆锥形仓库用于贮藏食盐(供融化高速公路上的积雪之用),已建的仓库的底面直径为12M,高4M。养路处拟建一个 更大的圆锥形仓库,以存放更多食盐。现有两种方案:一是新建的仓库的底面直径比原来大4M(高不变);二是
更大的圆锥形仓库,以存放更多食盐。现有两种方案:一是新建的仓库的底面直径比原来大4M(高不变);二是 高度增加4M(底面直径不变)。
高度增加4M(底面直径不变)。
(1)分别计算按这两种方案所建的仓库的体积;
(2)分别计算按这两种方案所建的仓库的表面积;
(3)哪个方案更经济些,说明理由.
如图:一个圆锥的底面半径为2,高为6,在其中有一个半径为x的内接圆柱。
(1)试用x表示圆柱的体积;
(2).当x为何值时,圆柱的侧面积最大,最大值是多少。
已知函数 (
( 为实数,
为实数, ,
, ).
).
(1)当函数 的图像过点
的图像过点 ,且方程
,且方程 有且只有一个根,求
有且只有一个根,求 的表达式;
的表达式;
(2)若 当
当 ,
,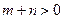 ,
, ,且函数
,且函数 为偶函数时,试判断
为偶函数时,试判断 能否大于
能否大于 ?
?