(本小题满分12分)
如图,反比例函数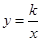 的图象经过A、B两点,根据图中信息解答下列问题:
的图象经过A、B两点,根据图中信息解答下列问题: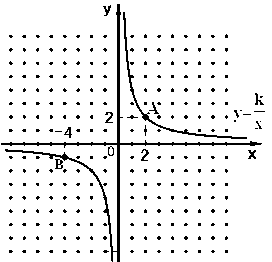
(1)写出A点的坐标;
(2)求反比例函数的解析式;
(3)若点A绕坐标原点O旋转90°后得到点C,请写出点C的坐标;并求出直线BC的解析式.
(本小题满分10分)
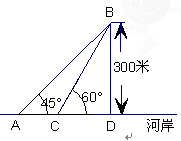
如图,某地海岸线可以近似地看作一条直线,两救生员在岸边A处巡查,发现在海中B处有人求救,救生员甲与乙都没有直接从A处游向B处,甲是沿岸边A处跑到离B最近的D处,然后游向B处;乙是沿岸边A处跑到点C处然后游向B处,若两救生员在岸边的行进速度都为6米∕秒,在海水中的行进速度都为2米∕秒,试分析救生员的选择是否正确?谁先到达点B处?(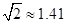 ,
,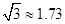 )
)
(本题满分10分第(1)小题满分4分,第(2)小题满分3分,第(3)小题满分3分)
某中学对全校学生60秒跳绳的次数进行了统计,全校平均次数是100次.某班体育委员统计了全班40名学生60 秒跳绳的成绩,列出的频数分布直方图如下(每个分组包括左端点,不包括右端点),那么
秒跳绳的成绩,列出的频数分布直方图如下(每个分组包括左端点,不包括右端点),那么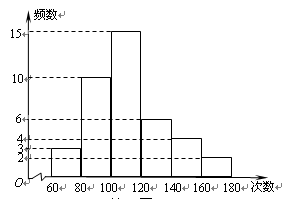
(1)该班60秒跳绳的平均次数至少是 ▲.
(2)该班学生跳绳成绩的中位数所在范围是 ▲.
(3)从该班中任选一人,其跳绳次数达到或超过校平均次数的概率是 ▲.
(本小题满分8分)如图,∠ABC=90°,AB=BC.
(1)画四边形ABCD,使AD>CD,且∠ADC=90°,再画点B到AD的垂线段BE,垂足为E.
(2)在四条线段AE,BE,CD,DE中,某些线段之间存在一定的数量关系.请你写出两个等式分别表示这些数量关系(每个等式中含有其中的2条或3条线段),并任选一个等式说明等式成立的理由.
(本小题满分6分)某市大道快速公交(简称BRT)试验线道路改造工程中,某工程队小分队承担了100米道路的改造任务.为了缩短对站台和车道施工现场实施围蔽的时间,在确保工程质量的前提下,该小分队实际施工时每天比原计划多改造道路10米,结果提前5天完成了任务,求原计划平均每天改造道路多少米?