如图甲所示，相距为L的光滑平行金属导轨水平放置，导轨一部分处在以OO′为右边界匀强磁场中，匀强磁场的磁感应强度大小为B，方向垂直导轨平面向下，导轨右侧接有定值电阻R，导轨电阻忽略不计。在距边界OO′也为L处垂直导轨放置一质量为m、电阻r的金属杆ab。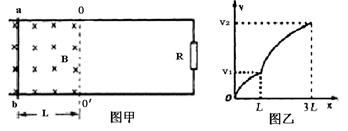
（1）若金属杆ab固定在导轨上的初位置，磁场的磁感应强度在t时间内由B均匀减小到零，求此过程中电阻R上产生的电量q。
（2）若ab杆在恒力作用下由静止开始向右运动3L距离，其速度—位移的关系图象如图乙所示（图中所示量为已知量）。求此过程中电阻R上产生的焦耳热Q1。
（3）若ab杆固定在导轨上的初始位置，使匀强磁场保持大小不变绕OO′轴匀速转动。若磁场方向由图示位置开始转过
的过程中，电路中产生的焦耳热为Q2. 则磁场转动的角速度ω大小是多少？
一横截面积为S的汽缸水平放置，固定不动，汽缸壁是导热的，两个活塞A和B将汽缸分隔为1、2两气室，达到平衡时1、2两气室体积之比为3∶2，如图13所示．在室温不变的条件下，缓慢推动活塞A，使之向右移动一段距离d，求活塞B向右移动的距离，不计活塞与汽缸壁之间的摩擦．
重1 000 kg的气锤从2.5 m高处落下，打在质量为200 kg的铁块上，要使铁块的温度升高40℃，气锤至少应落下多少次？(设气锤撞击铁块时做的功有60%用来使铁块温度升高，且铁的比热c＝0.11 cal/(g·℃)，1 cal＝4.2 J，g取10 m/s2)
一铁球从高H处由静止落到地面上，回弹速率是落地速率的一半，设撞击所转化的内能全部使铁球温度升高，则铁球的温度升高多少？(设铁的比热容为c，各物理量取国际制单位)
一定量的气体从外界吸收了2.6×105 J的热量，内能增加了4.2×105 J，是气体对外界做了功，还是外界对气体做了功？做了多少功？如果气体吸收的热量仍为2.6×105 J不变，但是内能只增加了1.6×105 J，这一过程做功情况怎样？
空气压缩机在一次压缩中，活塞对空气做了2×105 J的功，同时空气的内能增加了1.5×105 J，这一过程中空气向外界传递的热量是多少？