如图所示，光滑水平面上有A、B、C三个物块，其质量分别为mA =2kg，mB =1kg，mC =1kg．现用一轻弹簧将A、B两物块连接，并用力缓慢压缩弹簧使A、B两物块靠近，此过程外力做功W=108J（弹簧仍处于弹性限度内），然后同时释放A、B，弹簧开始逐渐变长，当弹簧刚好恢复原长时，C恰以4m/s的速度迎面与B发生碰撞并粘连在一起．求：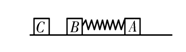
①弹簧刚好恢复原长时（B与C碰撞前）A和B物块速度的大小？
②当弹簧第二次被压缩到最短时，弹簧具有的弹性势能为多少？
在研究某些物理问题时，有很多物理量难以直接测量，我们可以根据物理量之间的定量关系和各种效应，把不容易测量的物理量转化成易于测量的物理量。
（1）在利用如图1所示的装置探究影响电荷间相互作用力的因素时，我们可以通过绝缘细线与竖直方向的夹角来判断电荷之间相互作用力的大小。如果A、B两个带电体在同一水平面内，B的质量为m，细线与竖直方向夹角为θ，求A、B之间相互作用力的大小。
（2）金属导体板垂直置于匀强磁场中，当电流通过导体板时，外部磁场的洛伦兹力使运动的电子聚集在导体板的一侧，在导体板的另一侧会出现多余的正电荷，从而形成电场，该电场对运动的电子有静电力的作用，当静电力与洛伦兹力达到平衡时，在导体板这两个表面之间就会形成稳定的电势差，这种现象称为霍尔效应。利用霍尔效应可以测量磁场的磁感应强度。
如图2所示，若磁场方向与金属导体板的前后表面垂直，通过所如图所示的电流I，可测得导体板上、下表面之间的电势差为U，且下表面电势高。已知导体板的长、宽、高分别为a、b、c，电子的电荷量为e，导体中单位体积内的自由电子数为n。求：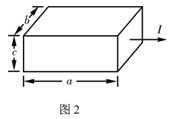
a．导体中电子定向运动的平均速率v；
b．磁感应强度B的大小和方向。
如图所示，MN、PQ是两根足够长的光滑平行金属导轨，导轨间距为d，导轨所在平面与水平面成θ角，M、P间接阻值为R的电阻。匀强磁场的方向与导轨所在平面垂直，磁感应强度大小为B。质量为m、阻值为r的金属棒放在两导轨上，在平行于导轨的拉力作用下，以速度v匀速向上运动。已知金属棒与导轨始终垂直并且保持良好接触，重力加速度为g。求：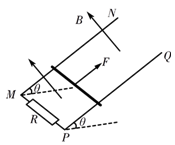
（1）金属棒产生的感应电动势E；
（2）通过电阻R电流I；
（3）拉力F的大小。
(15分) 如图所示，质量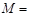
20kg的物体从光滑斜面上高度
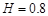m处释放，到达底端时水平进入水平传送带(不计斜面底端速度大小的损失,即在斜面底端速度方向迅速变为水平,大小不变)，传送带由一电动机驱动着匀速向左转动，速率为3 m/s．已知物体与传送带间的动摩擦因数
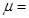0.1. 物体冲上传送带后就移走光滑斜面.（g取10 m/s2）.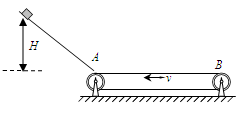
（1）物体滑上传送带A点时的速度大小。
（2）若两皮带轮AB之间的距离是6 m，物体将从哪一边离开传送带?
（3）若皮带轮间的距离足够大，从M滑上到离开传送带的整个过程中，求M和传送带间相对位移.
一质量m＝0.5kg的滑块以一定的初速度冲上一倾角为30°足够长的斜面，某同学利用DIS实验系统测出了滑块冲上斜面过程中多个时刻的瞬时速度，如图所示为通过计算机绘制出的滑块上滑过程的v－t图象(g取10m/s2)．求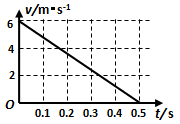
(1)滑块冲上斜面过程中加速度的大小；
(2)滑块与斜面间的动摩擦因数；
(3)判断滑块最后能否返回斜面底端．若能返回，求出滑块返回斜面底端时的速度；若不能返回，求出滑块所停位置．
如图所示，细绳OA的O端与质量
的重物相连，A端与轻质圆环（重力不计）相连，圆环套在水平棒上可以滑动；定滑轮固定在B处，跨过定滑轮的细绳，两端分别与重物m、重物G相连，若两条细绳间的夹角
，OA与水平杆的夹角
圆环恰好没有滑动，不计滑轮大小，整个系统处于静止状态，滑动摩擦力等于最大静摩擦力．（已知
;
）：
（1）圆环与棒间的动摩擦因数
；（2）重物G的质量M