根据下表中一次函数的自变量x与函数y的对应值,可得p的值为( )
| x |
-2 |
0 |
1 |
| y |
3 |
p |
0 |
A.1
B.-1
C.3
D.-3
已知点A(0,0),B(0,3),C(4,t+3),D(4,t) 记N(t)为□ABCD内部(不含边界)整点的个数,其中整点是指横坐标和纵坐标都是整数的点,则N(t)所有可能的值为
| A.6、7 | B.7、8 | C.6、7、8 | D.6、8、9 |
如图,在菱形纸片ABCD中,∠A=60°,将纸片折叠,点A、D分别落在点A′、D′处,且A′D′经过点B,EF为折痕,当D′F⊥CD时,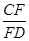 的值为()
的值为()
A.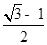 B.
B.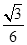 C.
C. D.
D.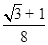
如图,在平面直角坐标系中,点A的坐标为(0,3),△OAB沿x轴向左平移后得到△O′A′B′,点A的对应点在直线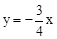 上一点,则点B与其对应点B′间的距离为()
上一点,则点B与其对应点B′间的距离为()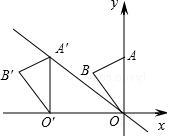
A.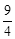 |
B.3 | C.4 | D.5 |
根据指令[s,A](s≥0,0°<A≤360°),机器人在平面上完成下列动作:先原地逆时针旋转角度A,再朝其面对的方向行走s个单位.现机器人在平面直角坐标系的原点,且面对x轴的正方向,如果输入指令为[1,45°],那么连续执行三次这样的指令,机器人所在位置的坐标是()
A.(0, ) ) |
B.(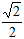 , ,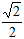 ) ) |
C.(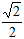 , ,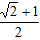 ) ) |
D.(0,1+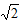 ) ) |
如图,一个半径为r的圆形纸片在边长为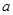 (
(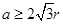 )的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“不能接触到的部分”的面积是()
)的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“不能接触到的部分”的面积是()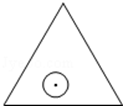
A.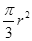 |
B.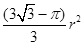 |
C.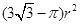 |
D.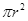 |