某校九年级小聪、小亮两位同学毕业评价的三项成绩如下表(单位：分)．学校规定：毕业评价成绩达80分以上(含80分)为“优秀”．
| 项目 |
综合素质 |
考试成绩 |
体育测试 |
| 满分 |
100 |
100 |
100 |
| 小聪 |
72 |
98 |
60 |
| 小亮 |
90 |
75 |
95 |
(1)若将三项成绩的平均分记为毕业评价成绩，则小聪、小亮谁能达到“优秀”水平？
(2)若综合素质、考试成绩、体育测试三项成绩按4︰4︰2计算毕业评价成绩，通过计算说明小聪和小亮谁能达到“优秀”水平．
在四边形ABCD中，对角线AC、BD相交于点O，将△COD绕点O按逆时针方向旋转得到△C1OD1，旋转角为θ（0°＜θ＜90°），连接AC1、BD1，AC1与BD1交于点P．
（1）如图1，若四边形ABCD是正方形．
①求证：△AOC1≌△BOD1．
②请直接写出AC1与BD1的位置关系．
（2）如图2，若四边形ABCD是菱形，AC=5，BD=7，设AC1=kBD1．判断AC1与BD1的位置关系，说明理由，并求出k的值．
（3）如图3，若四边形ABCD是平行四边形，AC=5，BD=10，连接DD1，设AC1=kBD1．请直接写出k的值和
的值．
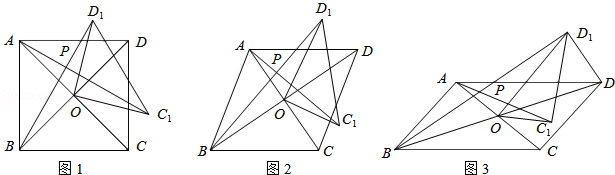
已知二次函数
（
为常数，且
）的图象过点A（0，1），B（1，-2）和点C（-1，6）．
（1）求二次函数表达式；
（2）若
，比较
与
的大小；
（3）将抛物线平移，平移后图象的顶点为
，若平移后的抛物线与直线
有且只有一个公共点，请用含
的代数式表示
．
（1）如图1，在四边形ABCD中，AB＝AD，∠BAD＝120°，∠B＝∠ADC＝90°，EF分别是 BC，CD上的点，且∠EAF＝60°，探究图中线段BE，EF，FD之间的数量关系．
小王同学探究此问题的方法是延长FD到点G，使DG＝BE，连结AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论应是；
探索延伸：
（2）如图2，若在四边形ABCD中，AB＝AD，∠B＋∠D＝180°，E，F分别是BC，CD上的点，且∠EAF＝
∠BAD，上述结论是否仍然成立，并说明理由．
如图，在△ABC中，∠ABC=90°，以AB为直径的⊙O与边AC交于点D，过点D的直线交BC边于点E，∠BDE=∠A．
（1）证明：DE是⊙O的切线；
（2）若⊙O的半径R=5，tanA=
，求线段CD的长．
国家海洋局将中国钓鱼岛最高峰命名为“高华峰”，并对钓鱼岛进行常态化立体巡航．如下图，在一次巡航过程中，巡航飞机飞行高度为2001米，在点A处测得高华峰顶F点的俯角为30°，保持方向不变又前进1200米到达点B处测得F点的俯角为45°．请据此计算高华峰的海拔高度．（结果保留整数，参考数值：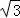
≈1．732）